Nanoscale Phonon Transport
Introduction
When phonon mean free paths become close to, or smaller than, the characteristic system lengthscale, Fourier's heat conduction law fails. The resulting kinetic behavior can be captured using a Boltzmann transport equation (BTE) for phonons. Modeling at the kinetic level allows the treatment of device-level lengthscales that are too expensive to treat using atomistic modeling.
Efficient phonon simulation using deviational methods
Our group focuses on developing and using efficient methods for simulating heat transport at these lengthscales. The video below shows three-dimensional phonon transport simulations of Transient Thermo-reflectance experiments (as applied to thermal conductivity spectroscopy) using the deviational method developed by our group [1]. Due to the small temperature differences present in this problem, simulation using traditional Monte Carlo methods is impossible.
Movie Caption: Boltzmann solution for the temperature field in Thermal Conductivity Spectroscopy, whereby a short laser pulse heats a thin aluminum film deposited on a silicon substrate. The small resulting temperature differences can be captured using the variance reduction methodologies developed by our group. Prepared by J.P. Péraud.
Deviational methods are described in more detail in section "Variance Reduction".
A Simpler, more efficient simulation method
In problems where temperature differences are small, additional computational benefits can be obtained by linearizing the governing (Botzmann) equation. One class of methods that take advantage of linearity uses adjoint formulations [5] and is discussed below. Additional computational benefits, unique to the phonon Boltzmann equation, can be obtained by noticing [2] that particles simulating the deviation from equilibrium in energy-based formulations [1] can be treated independently. The resulting technique [2,3] is typically several orders of magnitude more efficient than the one described in [1] as shown in the comparison below (for the same cost, it can reach significantly longer timescales).
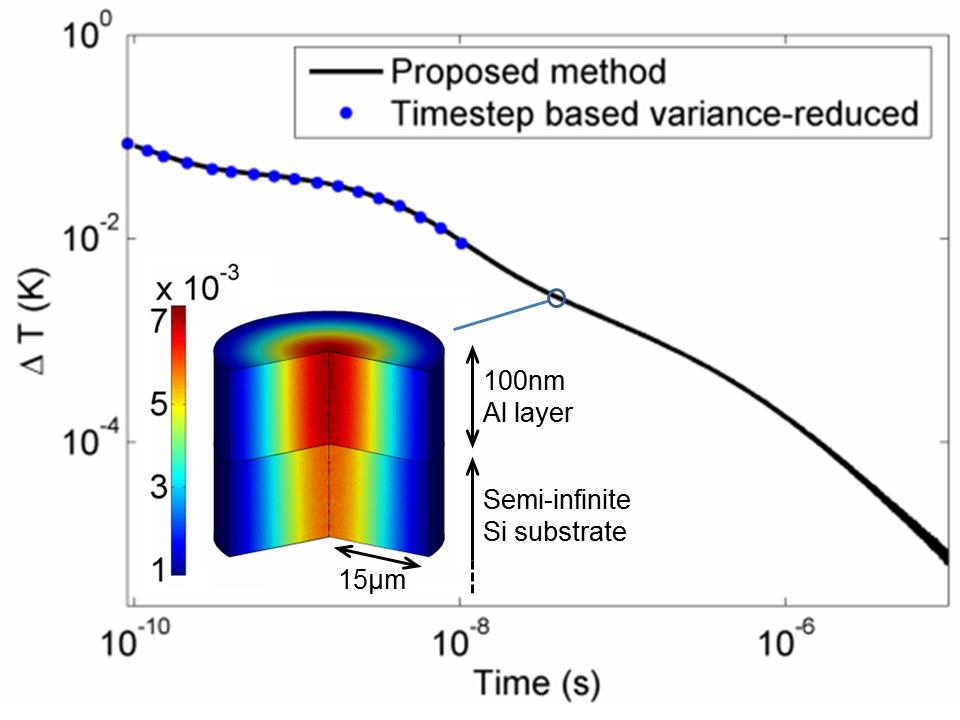
Adjoint-based Deviational Simulations
Adjoint methods exploit the linearity of the linearized Boltzmann equation to provide additional computational benefits in problems where reversing particle trajectories provides an advantage. Adjoint methods can be very beneficial in problems where the solution is required over very small regions of phase space, thus restiricting the opportunity for sufficient averaging. The adjoint formulation [5] shows that the required answer can be obtained without approximation by considering the motion of particles moving backwards in time. In cases where the sources of particles are much larger than the detectors, this technique can improve the signal to noise ratio significantly and in some cases make previously intractable problems tractable.
Mean Free Path Reconstruction using Solutions of the Botzmann Equation
Transient thermoreflective experiments are used to extract the phonon free path distribution in materials from measurments of their thermal response. Using the efficient methods for simulating the Boltzmann equation described above (and in particular the adjoint-based method [5]), we have developed an optimization-based approach for reconstructing the material free path distribution [6] that does not make use of the approximate effective thermal conductivity assumption.
Asymptotic Solution of the Boltzmann Equation and Kinetic Extensions of Fourier's Law
In analogy to slip-flow in nanoscale fluid dynamics, the validity of Fourrier's law can be extended by finding the equation and boundary conditions governing heat transfer via asymptotic solution of the Boltzmann equation in the Kn <<1 limit. In [7] we develop an asymptotic treatment to show that solutions of the Boltzmann equation can be recovered by solving the heat conduction equation subject to no-jump boundary conditions to zeroth order and jump borundary conditions to higher order in Kn. We also show how jump relations, coefficients, and associated Knudsen layers can be derived. Finally we show that the temperature jump and kapitza resistance associated with an interface can be described accurately by an asymptotic solution of this type.
Related Publications:
1. Péraud, J-P.M. and N.G. Hadjiconstantinou, "Efficient simulation of multidimensional phonon transport using energy-based variance-reduced Monte Carlo formulations," Physical Review B, 84, 205331, 2011. (view)
2. Péraud, J-P.M. and N.G. Hadjiconstantinou, "An alternative approach for efficient simulation of micro/nanoscale phonon transport," Applied Physics Letters, 101, 153114, 2012. (view)
3. Péraud, J-P.M, Landon, C.D. and Hadjiconstantinou, N.G. Monte Carlo Methods for Solving the Boltzmann Transport Equation, Annual Review of Heat Transfer, 17, 205-265, 2014. (view)
4. Landon, C.D. and Hadjiconstantinou, N.G., Deviational Simulation of Phonon Transport in Graphene Ribbons with Ab Initio Scattering, Journal of Applied Physics 116, 163502, 2014. (view)
5. Péraud, J-P. M and Hadjiconstantinou, N.G., Adjoint-based Deviational Monte Carlo Methods for Phonon Transport Calculations, Physical Review B, 91, 235321, 2015. (view)
6. Forghani, M., Hadjiconstantinou, N.G. and J-P.M. Péraud, Reconstruction of the Phonon Relaxation Times using Solutions of the Boltzmann Transport Equation, Physical Review B, 94, 155439, 2016. (view)
7. Péraud, J-P. M and Hadjiconstantinou, N.G., Extending the Range of Validity of Fourier's Law into the Kinetic Transport regime via Asymptottic Solution of the Phonon Boltzmann Transport Equation, Physical Review B, 93, 045424, 2016. (view)

