Specific Aim: A membrane-field interaction model will be developed to study the changes in membrane electrical properties and the dynamics of membrane pores in the presence of an electric field. This model will couple the spatial distribution of membrane potential to that of membrane pores. The principles of cable theory will be used to express the transmembrane potential distribution. The pore population dynamics will be determined using the aqueous pore theory (Barnett and Weaver, 1991).
Preliminary Studies: The specific aim of this project is to construct a model that will encompass changes in membrane properties and distribution of membrane pores. Such a model was developed based on the principles of cable theory and of membrane pore theory of Barnett and Weaver (1991).

 and
and  , respectively. The cell membrane is represented by a network of
parallel resistors (
, respectively. The cell membrane is represented by a network of
parallel resistors ( ) and capacitors (
) and capacitors ( ), with a transmembrane
potential
), with a transmembrane
potential  across the membrane. The long axis of the cylindrical
cell is assumed to be along the z-direction.
across the membrane. The long axis of the cylindrical
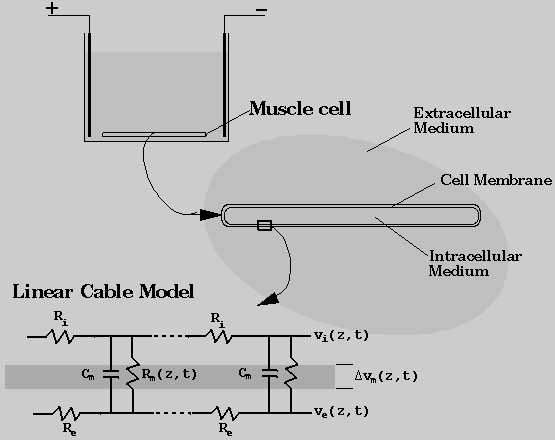
cell is assumed to be along the z-direction. The system modeled in this project parallels the experimental arrangement shown in Fig. 1. A long skeletal muscle cell was assumed to be placed in a conducting medium between two parallel electrodes. The effects of an applied electric field on the properties of the cell membrane was modeled as a coupled process involving aqueous pore formation and generation of elevated transmembrane potentials. Membrane poration was described in terms of the presence of transient aqueous pores on the membrane. Changes in transmembrane potential distribution was determined using a non-uniform cable model.
Non-Uniform Cable Model
Using the cable theory, the electrical properties of a cell membrane were represented by a series of parallel resistors and capacitors (Rall, 1977), as illustrated in Fig. 1. In this model, the cell membrane was treated as a highly insulating cylindrical boundary separating two electrical conductors that represent the intracellular and extracellular fluids. The potential across the membrane can be expressed as the sum of resting and induced membrane potentials. Assuming that the interior of the cell is at isopotential, the induced membrane potential is a function of the applied electric field. When the resting membrane potential is zero, the induced membrane potential is linearly proportional to the applied voltage assuming that the membrane is uniformly of very low conductivity. For the case of a conducting membrane with spatially non-uniform properties, the membrane potential distribution can be described by the cable theory.
Using circuit theory, the induced transmembrane
potential  under an applied field along the z-direction
at time t was represented by the partial differential equation:
under an applied field along the z-direction
at time t was represented by the partial differential equation:
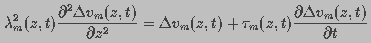 (1)
(1)
 and
and 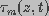 are the dimensionless
space constant and time constant, respectively, given by
are the dimensionless
space constant and time constant, respectively, given by
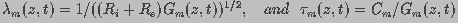 (2)
(2)
 and
and
 are the resistances of the intracellular and
extracellular fluids, respectively, and
are the resistances of the intracellular and
extracellular fluids, respectively, and  and
and  (=1/
(=1/ )
are the capacitance and conductance of the membrane, respectively. The
membrane conductance, reciprocal of the membrane resistance,
)
are the capacitance and conductance of the membrane, respectively. The
membrane conductance, reciprocal of the membrane resistance,  is a function of the spatial distribution of aqueous
pores on the membrane and is given by
is a function of the spatial distribution of aqueous
pores on the membrane and is given by
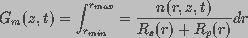 (3)
(3)
 and
and  are the minimum and maximum pore radii.
are the minimum and maximum pore radii.
 and
and  are the spreading and pore resistances given by
are the spreading and pore resistances given by
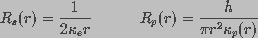 (4)
(4)
 and
and
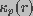 denote the conductivity of bulk medium and the conductivity of
a pore of radius r, respectively. Equation 1 does not take into
account the effect of resting membrane potential that arises in addition
to the pore conductance considered in this model. A modification to
the above equation will be incorporated into the model.
denote the conductivity of bulk medium and the conductivity of
a pore of radius r, respectively. Equation 1 does not take into
account the effect of resting membrane potential that arises in addition
to the pore conductance considered in this model. A modification to
the above equation will be incorporated into the model. In the traditional uniform cable theory, space and time constants are spatially invariant. Such a treatment is valid only under steady-state conditions. In this model, these parameters are dependent on membrane conductance which, in turn, depends on the pore density. Thus, space and time constants are treated as spatially and temporally varying parameters.
Initial and Boundary Conditions: In order to determine an
initial condition for solving the above differential equation, it was assumed
that a spatial change in the induced transmembrane potential was due solely to the
applied electric field. For the isolated cell case, it was assumed that the
extracellular current was far greater than the intracellular
current, i.e.,  , because the extracellular
space is much larger than the intracellular space. Therefore, the product
, because the extracellular
space is much larger than the intracellular space. Therefore, the product
 was assumed to be constant and equal to the applied
field strength,
was assumed to be constant and equal to the applied
field strength,  , i.e.,
, i.e.,
 . This led to
. This led to
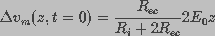 (5)
(5)
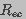 is the resistance of each of the two hemispherical
regions that constitute the endcaps (ec) of the cell
(Gaylor et al. 1988).
is the resistance of each of the two hemispherical
regions that constitute the endcaps (ec) of the cell
(Gaylor et al. 1988).
The boundary condition constraining  is written, using
Kirchhoff's voltage law and charge conservation, as:
is written, using
Kirchhoff's voltage law and charge conservation, as:
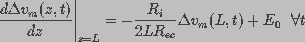 (6)
(6)
 ,
where z=0 refers to the center of the cell.
,
where z=0 refers to the center of the cell. The second-order partial differential equation (Eq. 1) describes the spatial distribution of transmembrane potential under an applied field. This is coupled to the pore distribution through the spatially and temporally varying space and time constants. These parameters are determined from pore distribution using the membrane pore model.
Membrane Pore Model
Transmembrane potential distribution obtained from linear cable theory was used to evaluate a corresponding pore distribution. Creation, destruction, and evolution of membrane pores were modeled using the aqueous pore theory.
Following the approach developed by Barnett and Weaver (1991), the evolution of aqueous pores on the cell membrane was modeled as a transmembrane potential-driven process. According to this model, the cell membrane was assumed to contain random local thermal defects or pores. The presence of a energy gradient causes the pressure inside a pore to exceed that of the surrounding bath. The pressure difference drives the water molecules out of the pore and causes the pore to contract. On the other hand, the expansion of a pore occurs as a result of the movement of water molecules into the pore. The energy gradient is very large under quiescent conditions which prevents the pores from expanding to a larger radius. However, the application of an external electric field elevates the transmembrane potential thus lowering the energy gradient. Thus, an increased transmembrane potential induces the expansion of a pore.
A change in pore density occurs due to the difference between expanding and restoring forces. Diffusion of water contributes to both expansion and contraction of a pore. This can be expressed in the form of a convection-diffusion equation. Let n(r,z,t)dr be the number of pores in the membrane with radius between r and r+dr at time t within a unit area of the membrane around z. The total change in n(r,z,t) is described by Smoluchowski equation (Gardiner, 1985)
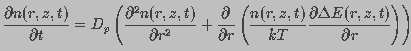 (7)
(7)
 represents the effective diffusion coefficient of a
membrane pore in radius space,
represents the effective diffusion coefficient of a
membrane pore in radius space, 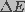 is the pore energy,
kT is the product of Boltzmann's constant and temperature (in
is the pore energy,
kT is the product of Boltzmann's constant and temperature (in
 ).
).
Pore energy, 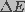 , denotes the energy required to
form a pore of
a given radius, r. It can be described as the sum of a mechanical
(
, denotes the energy required to
form a pore of
a given radius, r. It can be described as the sum of a mechanical
( ) and an electrical (
) and an electrical ( ) component.
The mechanical energy describes the balance between expanding and restoring
surface tension forces on the pore wall. The electrical energy relates
to the transmembrane potential-induced expansive force. The pore energy,
) component.
The mechanical energy describes the balance between expanding and restoring
surface tension forces on the pore wall. The electrical energy relates
to the transmembrane potential-induced expansive force. The pore energy,
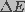 , is a function of pore radius r and
transmembrane potential
, is a function of pore radius r and
transmembrane potential  and is given by
and is given by
 (8)
(8)
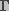 is the surface tension of the membrane-water
interface, and
is the surface tension of the membrane-water
interface, and  is the edge energy of the pore. In
the above equation,
is the edge energy of the pore. In
the above equation,  and
and  denote the dielectric constant of water and lipid,
respectively and
denote the dielectric constant of water and lipid,
respectively and 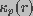 and
and  are
the conductivities of a pore of radius r and of the bulk
electrolyte medium.
are
the conductivities of a pore of radius r and of the bulk
electrolyte medium.
Initial and Boundary Conditions: In order to solve
Smoluchowski equation (Eq. 7), the following
constraints were introduced. It was assumed that no pores of size
 exist and that the number of pores changed within a given time
interval due to creation and destruction of pores of radius
exist and that the number of pores changed within a given time
interval due to creation and destruction of pores of radius  giving the boundary condition
giving the boundary condition
 (9)
(9)
 and
and 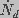 are the creation and destruction rates
of pores of radius
are the creation and destruction rates
of pores of radius  and J is the flux of pores
in radius space, given by
and J is the flux of pores
in radius space, given by
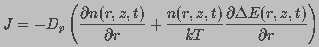 (10)
(10)
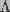 , a sum of two terms,
one dependent on transmembrane potential and the other independent of the
potential, such that
, a sum of two terms,
one dependent on transmembrane potential and the other independent of the
potential, such that  .
Here,
.
Here,  is the voltage independent component of the energy barrier
to pore creation, and a is the capacitance associated with a
hydrophobic
pore that is subsequently converted to a hydrophilic pore. The pore creation
rate can be written as
is the voltage independent component of the energy barrier
to pore creation, and a is the capacitance associated with a
hydrophobic
pore that is subsequently converted to a hydrophilic pore. The pore creation
rate can be written as
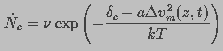 (11)
(11)
 is the attempt rate of thermal fluctuations and is a constant with dimensions of inverse
time. Assuming that the probability that a pore of radius
is the attempt rate of thermal fluctuations and is a constant with dimensions of inverse
time. Assuming that the probability that a pore of radius  is destroyed is independent of
is destroyed is independent of  , pore destruction rate
can be expressed as
, pore destruction rate
can be expressed as
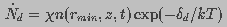 (12)
(12)
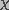 is the destruction rate prefactor with dimensions of velocity and
is the destruction rate prefactor with dimensions of velocity and
 is the voltage independent pore destruction rate.
Thus, the boundary condition at
is the voltage independent pore destruction rate.
Thus, the boundary condition at  was
was
 (13)
(13)
The probability that a large pore  will decrease in
size is very small. Thus, an "absorbing wall" condition,
n(r,z,t)=0 was used at
will decrease in
size is very small. Thus, an "absorbing wall" condition,
n(r,z,t)=0 was used at  . Here,
. Here,  was
assumed to equal
was
assumed to equal  , greater than the radius corresponding
to the radius of energy maximum at
, greater than the radius corresponding
to the radius of energy maximum at  .
.
At t=0, the membrane was assumed to be in equilibrium with
 .
The quasi-steady state solution of Smoluchowski equation under this
constraint, found analytically was
.
The quasi-steady state solution of Smoluchowski equation under this
constraint, found analytically was
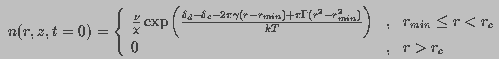 (14)
(14)
 is the critical radius of a pore.
is the critical radius of a pore. The coupling between membrane properties and field-induced pore population is two-fold. First, the space and time constants depend on membrane conductance which, in turn, is a function of pore density. Second, the pore energy, which governs the changes in pore population, is a function of transmembrane potential. Thus, Eq. 1 and Eq. 7 together describe a strongly coupled system. Solving these coupled differential equations permits the determination of pore population in terms of measurable quantities such as transmembrane current and potential.