The Darwinian revolution of the mid-Nineteenth Century produced a new science --- "biology" --- the practitioners of which received much less formal training in mathematics than had the older natural historians. ("Mathematics" here excludes the young field of statistics, which biologists not only studied, but helped to create.) The non-mathematical character of biology, along with its hostility to revealed religion and its shockingly brutal experimental methods, led many British physicists and mathematicians in the second half of the long century to reject and oppose it. Science, for the old guard, had to be quantitative, and to make numerically exact predictions; biology, therefore, was no science.
In practice, despite having survived the rigours of the Cambridge Tripos, the botanising vicars who dominated pre-Darwinian life science were no more quantitative than their materialist successors (nor did the Victorian theoretical physicists, for all their criticism of the new biology, come up with a more "scientific" alternative). At best, there was a tradition of noting geometrical or arithmetical patterns in life --- often quite surprising ones. The naturalists saw these patterns as evidence of a divine plan, but (unlike their cousins the astronomers) they never developed an elaborate theory to explain them or to make predictions, and the mathematics they employed was fairly unsophisticated compared to what they must have learned at University.
Later biologists, while acknowledging the existence of these patterns, mostly ignored them (with D'Arcy Wentworth Thompson the exception proving the rule, as we will see in a later blog-entry). In the Twentieth Century, a few biologists returned to the subject, as did some of the greatest mathematicians of all time --- Turing and von Neumann between them invented computer science almost accidentally while exploring the problem of biological order. Their disciples, however, were more interested in machines than in organisms, and only now is the topic finally attaining the attention it deserves.
Returning, however, to the infancy of the field, is no long trip: little progress has been made. The writings of the old naturalists can still serve as an excellent introduction.
George Dickie was a Scottish botanist who lived from 1812 to 1882. He was trained in the Christian/Platonist tradition -- the title of his 1856 book Typical Forms and Special Ends in Creation (co-authored with the logician and theologian James McCosh) speaks for itself -- but he was at home in the new scientific world of the High Victorians. As part of the elite team chosen to interpret the data collected by H.M.S. Challenger, he was present at the birth of deep-sea microbiology; his slides of diatoms can still be seen at the University of Dundee Museum. Late in life he was still thinking about the numerical regularities underlying the biological world, and wrote an essay on the subject for general readers in Robert Brown's remarkable collection Science for All [London: Cassell, Petter, & Galpin (1877)]. Much of it could have been written yesterday.
Dickie's words are in bold.
By George Dickie, M.A., M.D., F.L.S.
Emeritus Professor of Botany in the University of Aberdeen
The great variety in the external aspect or habit of plants has relation to several conditions, such as the character of the stem as regards height, branching, &c. ; the size, form, colour, and covering of leaves, and their arrangement on the stem : in the latter respect there is generally clear evidence of definite order or law.
The common observer may find a little difficulty at first in examining the subject, but some knowledge of it will add materially to the pleasure derived from the cultivation and examination of plants. We shall find that there is order in what looks at first sight most irregular, and that even the leaves of a plant are not attached to the stem without obeying certain fixed, though simple, mathematical laws.

Graphic by "Knulclunk"
It is necessary at the outset to explain a few technical terms used by botanists. The part of the stem or axis to which a leaf is attached, or from which it springs, is called a node ; the space or part of the axis between one node and the other, above or below, is called an internode, and these spaces are longer or shorter in different plants.
The relative positions of leaves on the axis, or the way in which they are distributed on the stem, is technically called phyllotaxis from two Greek words which signify leaf, and order or arrangement. Numerous treatises have been written on this subject by different observers, and it is considered to have relation to certain mathematical principles.
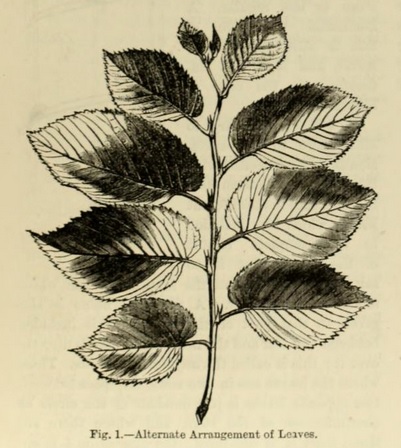
A very common arrangement is that which is called alternate (Fig. 1), in which the leaves stand singly on the nodes. Some common plants are examples, as the poplar, the oak, the apple, &c.
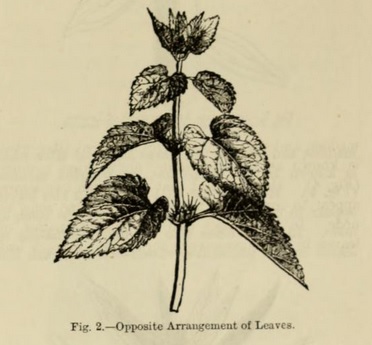
In other cases, a node appears to support two leaves --- one on one side, another on the other side of the axis : the term opposite is applied to such cases (Fig. 2).

Twayblade, Neottia (Listera) ovata. [Photo by Bernd Haynold]
In some cases a superficial examination might lead to an erroneous conclusion, the two leaves being nearly but not strictly in opposition ; the term sub-opposite would be the correct expression in such, there being in reality a short internode between the two. Two of our native orchids, such as the twayblade (Listera), not uncommon in shady meadows and woods, may be mentioned as examples ; and in a series of specimens a few may occur in which the leaves obviously come under the first or alternate arrangement, the internode being longer than usual.
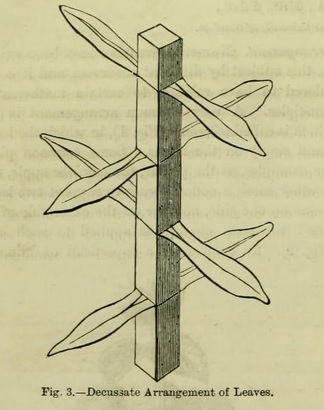
It is, however, worthy of notice that usually the pairs of opposite leaves alternate with each other --- that is to say, if we place the stem before us, and observe a pair of leaves one on the right, the other on the left, the next pair will stand one in front and the other behind ; the successive pairs of leaves are then described as decussate (Fig. 3), but even this may not be strictly true, and several pairs of leaves may intervene between those which are properly at right angles to each other.
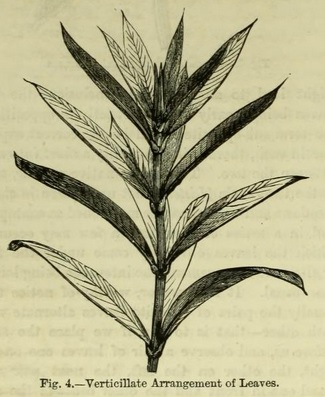
Take, again, the common bed-straw (Galium), or madder, and we find the leaves arranged after what is known as the verticillate, or whorled manner (Fig. 4). Here we find that more than two leaves appear to come from the same transverse zone, or node. In these cases also we find alternation of leaves in the successive whorls --- that is, each leaf usually stands opposite the spaces between the leaves of the next whorl.
Buttercup, from The Pictorial Flora by Mary Jackson [London: Longmans, 1840]
It has been already stated that the length of the internodes materially affects the habit or external aspect of plants, and there may be such difference of their length on the same axis and at different periods of its growth. In some of our common native species of buttercup, the leaves on the lower part of the stem appear to be in close tufts ; those further up are more widely separated, the internodes being longer.

Spiralling elm-leaves. [Photo by "Ptelea"]
If in the case of alternate leaves, like those of the elm or lime tree, we suppose a line drawn round the stem, and touching the point of attachment of each leaf, it will be seen to be a spiral line ; or fasten one end of a thread to the stalk of a leaf low down on the stem, then carry it to the next leaf above, and give it a twist or turn round the base of it, and so on ; the nature of the line of connection can then be seen : there is, in fact, a helix which, in passing round the stem, is more or less regular. A horizontal projection of this is called the genetic spiral, and it is best understood in the case of alternate leaves.
It will be necessary to allude here to an expression used in connection with this subject. The term cycle has reference to the different leaves which are included in the complete circuit of the spiral --- that is to say, those leaves from the first to the one which stands right above it.
A technical name is also given to that part of the stem or axis included between one leaf and the next which stands directly over it : this is called the angular divergence. Thus, where the leaves are in two rows, the space between two opposite leaves is just one-half of the circle or circumference of the stem, and where there are three rows it is one-third ; the expression "1/2" is applied in the first case, and "1/3" in the second. The upper figure (numerator) shows the number of turns in the helix, and the lower (denominator) the number of leaves embraced in the cycle.
A circle contains 360°; the term "1/2" indicates angular divergence equal to 180°, or one-half of 360° ; "1/3" corresponds to 120°, the third of a circle.
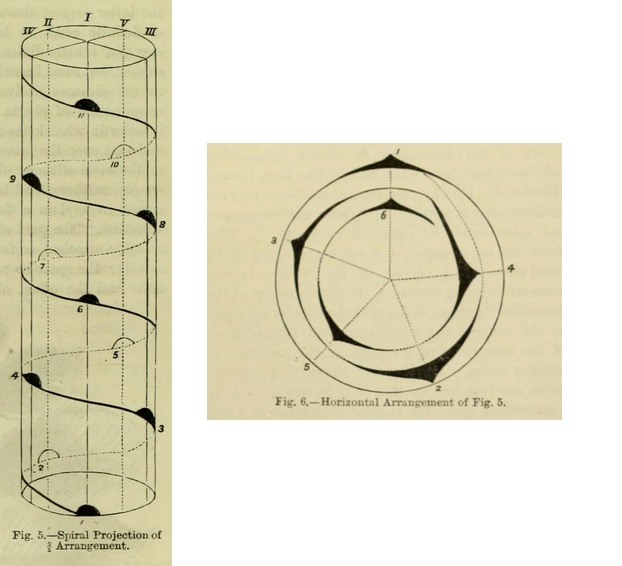
In many plants --- such as the apple, peach, cherry, poplar, &c. --- the leaves present a five-ranked arrangement. Beginning with one leaf, two circuits round the stem are necessary before reaching the leaf directly above the one from which the line began. The fraction "2/5" is used to indicate this --- that is to say, two turns round the stem, and the sixth leaf directly above the first ; therefore 5 leaves in the cycle. Figs. 5 and 6 show a spiral and horizontal projection of a 2/5 arrangement.
When we make three turns round the stem before reaching a leaf right above the first, the expression is "3/8", 3 being the number of turns, and 8 the number of leaves in the cycle.
There are other arrangements, and all may be set down here :
1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34, 21/55, &c.
Now, on examining these expressions, an interesting result comes out --- a fraction has its numerator equal to the sum of the numerators of the two preceding, and the same is true of the denominator.
One example may suffice. Taking the two first two --- 1/2, 1/3 --- these by addition [of the numerators and denominators separately] give the next 2/5, and so on. In the series given above, called the primary series, any numerator is the same as the denominator of the fraction next but one, preceding --- for example, the numerator in 2/5 is the denominator of the first, 1/2. [Although Dickie does not use the phrase, the sequence 1, 1, 2, 3, 5, 8, .... of course defines the Fibonacci numbers.]
A few examples may be given of plants which show .some of these arrangements :
- 1/2: Gladiolus, iris, grasses, lime, elm, &c.
- 1/3: Birch, orchis, tulip, &c.
- 2/5: Apple, oak, poplar, cherry, &c.
- 3/5: Flax, holly, &c.
- 5/13: Cones of Weymouth pines, eyes or buds on the tubers of potato plant.
- 8/21: Cones of larch and silver fir.
The more simple arrangements are of frequent occurence ; where the internodes are very short, the leaves are crowded, and the analysis of such cases is more difficult, as in the rosettes presented by the leaves of some sedums or stonecrops, and of sempervivum or houseleek (Fig. 7, showing 5/13 arrangement), and the cones of firs.
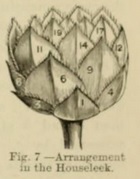
Nevertheless, the general spiral arrangements are in such cases obvious enough ; instead of one simple spiral there are several parallel or secondary spirals, more or less numerous. This is best seen in any large, or even small, fir-cone.
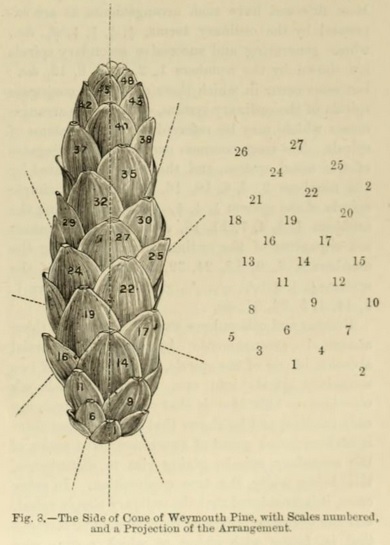
Some of the spirals run from left to right, others the reverse. In such cases the primary or generating spiral has reference to a full series of the leaves on the axis, the spiral line passing through every leaf ; the secondary spirals are only partial --- that is, do not embrace every leaf or scale. In such cases, the fundamental spiral cannot be easily followed; but an examination of the secondary spirals will give assistance in this. These secondary spirals vary in number according as the fractional sign of the primary spiral is higher.
The cone of Pinus strobus --- white or Weymouth pine --- is in various works used to illustrate this subject, and the same example may be adopted here. Fig. 8 represents one side of the cone with the scales numbered, and beside it a projection of the arrangement 5/13, the normal in this cone, the number 14 being directly above the scale number 1, the cycle consisting of 13 scales, the spirals being 5. A line which passes to the left through the numbers 1, 2, 3, 4, &c., makes five turns round the cone before it ends at 14, directly above 1. There are 5 parallel spirals of the order 1, 6, 11, &c. (these give the numerator), and 8 of the order 1, 9, 17, &c. ; then 8 and 5 give 13, so that the primary spiral expressed by 5/13 may be got from the number of secondary spirals parallel to one another.
Although the angular divergences of leaves represented by the series of fractions already given, are on the whole constant in individual plants, still it must be noted that there are deviations. Starting from one leaf, and following up the spiral, we may find a leaf vertically over the first, which will give a fraction different from the ordinary one, as has been shown in the case of some Firs by Professor A. Dickson [ On Some Abnormal Cones of Pinus pinaster by Alexander Dickson, Transactions of the Royal Society of Edinburgh 26, 505 (1872)].
Most fir-cones have such arrangements as are expressed by the ordinary terms, 1/2, 1/3, 2/5, 3/8, 5/13, &c., whose generating and successive secondary spirals are shown by the numbers 1, 2, 3, 5, 8, 13, &c. ; but cases occur in which there are either conjugate spirals of the ordinary system, or there are arrangements which may be referred to other systems of spirals. The more common exceptions are bijugates of the usual system, and therefore represented by the numbers 2, 4, 6, 10, 16, 26, &c. ; and simple spirals of the system 1/3, 1/4, 2/7, 3/11, 5/18, &c., giving the numbers 1, 3, 4, 7, 11, 18, &c. Rarer exceptions are trijugates of the ordinary system, giving the numbers 3, 6, 9, 15, 24, 39, &c., or spirals of the system 1/4, 1/5, 2/9, 3/14, 5/23, 8/37, giving the numbers 1, 4, 5, 9, 14, 23, 37, &c. [I have corrected numbers printed incorrectly in original.]
Bravais and others ...

The five Bravais lattices of the plane. [Drawing by "Prolineserver".]
[Yes, the same Bravais. The Brothers Bravais -- the famous crystallographer Auguste and the botanist Louis -- made one of the Nineteenth Century's few mathematically sophisticated efforts to understand biology. They concluded, perhaps inevitably in Auguste's case, that living matter is fundamentally crystalline.]
... Bravais and others have explained some of these abnormal arrangements by supposing partial abortion of one of the spirals, or coalescence of two secondary spirals into one. Professor Dickson's objection to this idea is that secondary spirals are only relative, and he shows that in some cases there is coalescence or union of two consecutive scales of the secondary spirals, giving rise to disturbance, this being really the true explanation. In other cases, it is considered that the ordinary simple spiral, and the ordinary bijugate, are fundamental forms --- that is, forms with either of which a cone may commence without the intervention of another. The derivations of the different systems from the one or from the other would thus be a simple matter.
Variations of the angular divergences of the
leaves of the Jerusalem Artichoke (Helianthus
tuberosus) have been examined by the Rev. George
Henslow.
[
On the Variations of the angular divergences of the Leaves
of Helianthus tuberosus by Rev. George Henslow,
Transactions of the Linnean Society 26, 647 (1870)]
He observed transitions from one kind
of divergence to another: 2/7, 3/11 were not uncommon,
and more rarely an approach to 1/4 and 5/18. But
these can be arranged in a series analogous to the
usual one --- viz., 1/4, 2/7, 3/11, 5/18 &c. ; that is to say,
numerators being the same, the denominators of the
successive fractions of the secondary series are equal
to the sums of the numerators and denominators
of the corresponding fractions of the ordinary or
primary series. Mr. Henslow shows that any one
series can pass into another if it be represented by
a generating spiral, the angular divergence of which
is a low one in that series. In the same paper a
comparative view is given of fractions belonging to
deviations from the ordinary or primary series,
thus : ---
Here the sum of the denominator and numerator
of the third fraction of the primary series gives the
denominator 7 to the third fraction of the secondary
series, and so on ; and, as in the primary series, so
in the others, the sum of the denominators of two
adjacent fractions gives the denominator of the next succeeding.
It has been already stated that in the primary series any numerator is the same number as the denominator of the fraction next but one preceding. This relation does not hold in the others ; "but if it be remembered that the denominators can be formed by adding the numerator and denominator of the corresponding fraction of the preceding series, the true and general relation at once appears."
The following are examples: --- The denominator of the fraction 3/8 supplies the numerator to the fraction 8/21 ; but iu the secondary series the denominator is 11 (i.e., 8 + 3); so also in the tertiary series the denominator of the corresponding fraction is 14 --- that is, 11 + 3 is equal to 8 + 3 + 3. The fourth fractions may, therefore, stand thus :
3/8, 3/(8+3), 3/(8+3+3), 3/(8+3+3+3), &c.
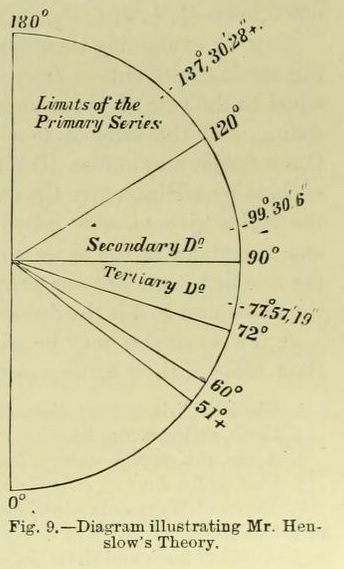
Mr. Henslow shows by a diagram (Fig. 9) that "the angular distances included by the limiting positions of the second leaves of all generating spirals, commencing at 0, decrease according as the spirals belong to the secondary, tertiary, or quaternary series ; so also does the number of leaves in a single coil increase correspondingly ; and, therefore, the higher the series, the more nearly does any spiral belonging to it approach the verticillate condition, provided the internodes be but slightly developed."
There appears to be a relation between the folding or mutual relation --- technically called œstivation or prefloration --- of the parts of the flower when in bud and the laws of phyllotaxis or leaf-arrangement. In many such flower-buds the arrangements 2/5, 3/8, 5/13 may be recognised; but to enter into details would necessitate the use of technicalities foreign to the subject of this article.
It may be stated here that in some of the lower forms of plants, such as mosses, ferns, &c., the angle of divergence of the leaf-organ is related to the principle of growth. In the 1/2 arrangement the cell at the end of the axis is divided into two. When the segmentation or division of the apical cell is in three rows, each new division-wall of the cell at the apex being parallel to the last division-wall but two, two rows of leaves are formed, arranged spirally with the divergence 1/3. The segmentation, then, of the apical cell has a relation to the leaf-arrangement in Cryptogams --- mosses, &c. ; in Phanerogams --- flowering plants --- the same relation does not hold.
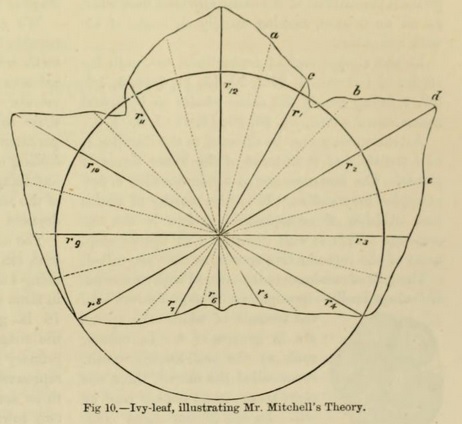
It may not be out of place to refer here to attempts having reference to approximate measurements of the mean curves of leaves. The subject has been examined by Mr. W. Mitchell ( On Approximate Measurements of the Axial Appendages of Plants by William Mitchell [Transactions of the Botanical Society of Edinburgh 6, 232 (1860)]).
Taking an outline of a leaf, he selects a point 1/4 of the mid-rib from the base, and from that he draws radii vectores to the outline, corresponding to equal arcs, into which a circle described round the pole or point is divided. On each side of these primary radii others are drawn at equal distances, and each measured by a scale of equal parts : the accompanying diagram (Fig. 10) of an ivy-leaf will illustrate the method.
The length of each principal radius, added to that of each of the secondary, and the sum divided by the total number, gives a mean radius to each primary division of the circle. It is conjectured that a series of careful measurements made in this way would afford data for comparing the average variation in form of the leaves of any plant, which might lead to numerical relations throwing light on the laws of vegetable morphology.
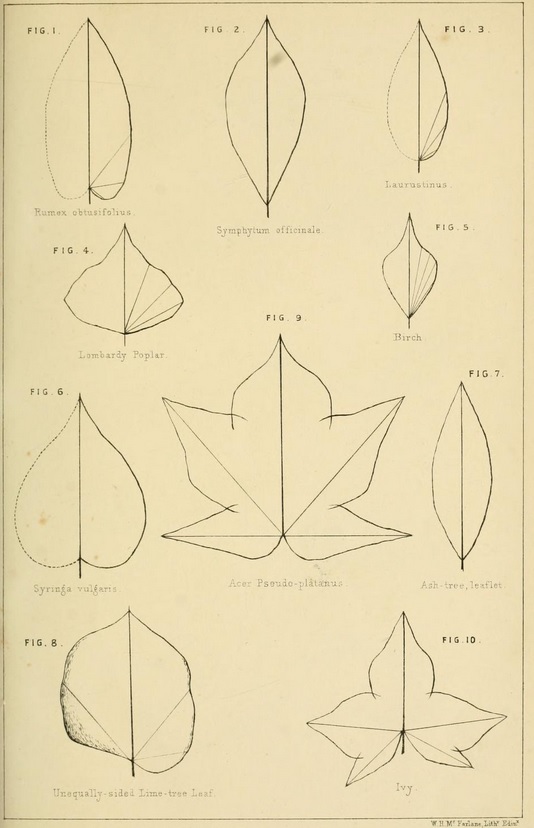

Mitchell's mathematically generated leaves.
In his second paper ( On Equations to the Curved Outlines of the Leaves of Plants by William Mitchell [Transactions of the Botanical Society of Edinburgh 10, 288 (1870)]) Mr. Mitchell treats of equations to the curved outlines of the leaves of plants. He proposes to find formulas to express the curves of the outlines of leaves, so that the calculated values should not differ from the measured, more than the proportional measurements of several leaves of the same plant differ among themselves, by reason of their ordinary variations.
He traces the outline of a well-developed leaf on paper. The base of the mid-rib is taken as the origin of measurement, and from it lines are drawn to the margin, making equal angles with each other. These being measured by a scale divided into tenths of an inch, and the first line or radius vector being longest, we have a descending series of terms from which to construct a formula for the curve in question, in simple, undivided leaves. Little modification is necessary to the more regularly divided leaves, and to compound leaves. In the 5-lobed leaf of maple, the radiating vein of each lobe may be compared to the mid-rib of a single leaf, and a formula found for 3 out of the 5. The intersections of the curves will produce the outline of the simple divided leaf, when set off on 5 axes, making usually an angle of 45° with each other.
In the simple leaf of laurustinus, the radii for angles of 10° are 34, 26.2, 20, 15, 11, 7.23, 5, 2.6, 0.2, 0, being nearly the same results as by actual measurement --- viz., 34, 26, 20, 15, 11, 7, 5, .2, 0.
[Here we see the surprising mathematical weakness of the
old natural historians. Dickie has taken these numbers directly
from Mitchell's paper: it will be noted that at least one entry
in the list must be missing, a typographical
error which Dickie seems to have overlooked,
suggesting he made no attempt to verify what he
is repeating. Moreover, the
calculated numbers are supposed to correspond to Mitchell's
formula
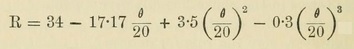
where θ is a multiple of 10°; this formula
actually generates 34, 26, 20, 15, 11, 8, 6, 4, 2, .2,
so Mitchell himself has made an arithmetical error.]
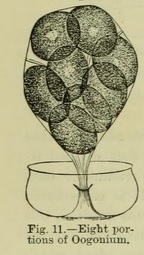
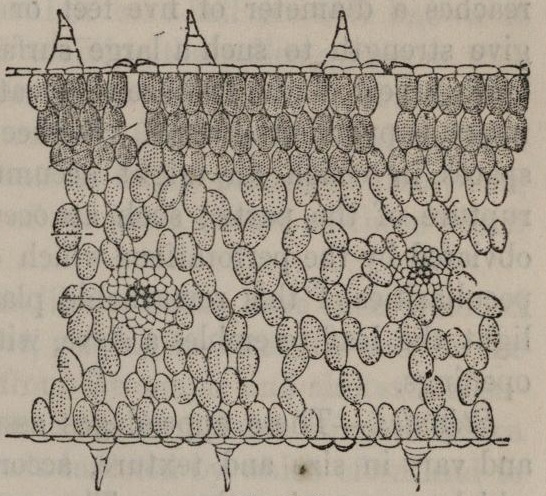
Attention may now be directed to the number 4, or a multiple of it in some of the lower forms of plants. The instances are so numerous that a few examples may suffice. It is also worthy of notice that division of protoplasm into two is not uncommon. This is well illustrated in the development of the reproductive spores, as they are called. The gills of mushrooms are covered with numerous club-shaped cells --- sporophores or spore-bearers --- on the summit of which the spores are in groups of 4. In others, such as the well-known mushroom called the morell, there are eight spores in an oblong case or cell. In one of our most common sea-weeds, the Fucus vesiculosus, or bladder fucus, so-called from numerous air-vesicles on it, the contents of oogonium divide into eight portions (Fig. 11).
The spores or seed-like organs of mosses, are produced in fours. In the common male fern, Aspidium filix mas., they follow the same law.
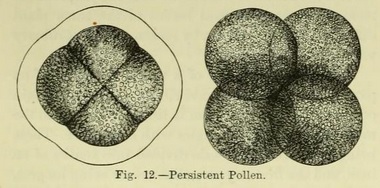
This is also illustrated in the development of the grains of the dust-like pollen, which is shaken out of the flowers of the higher plants, or those which have obvious flowers. This is well seen in the earlier stages of the pollen in mallow. After the four very young grains escape from the mother-cell and are free, they increase in size, and the surface becomes rough with projecting points. In some cases the grains, after escaping from the parent cell, even when mature, remain bound together, giving, thus, composite pollen. This occurs in species of typha (cat's-tail) or bullrush. An early stage of the pollen thus remains persistent (Fig. 12).

We may finally bring under notice the very notable law which prevails in the number of the teeth which surround the mouth of the ripe capsules or cases which contain the spores of mosses. It may be stated, in passing, that these teeth, forming what is called the peristome, are highly sensitive to moisture, folding over the mouth of the capsule, or unfolding outwards, according to the state of the atmosphere as regards moisture or dryness.
The numbers of these teeth, when present, are 4, or some power of 4 up to 64, being 4 in tetraphis (Fig. 1 3) ; 8 apparently in some species of orthotrichum (Fig. 14); 16 in grimmia and others ; in zygodon, the outer teeth are considered to be of 32 primary divisions, united 2 or 4 together, so as to represent 16 or 8 plain teeth. In polytrichum there are 64 (rarely 32) teeth. Where there are two rows of teeth, which is a frequent character, the law also prevails, and those of the one row alternate with those of the other.
If we examine the parts of the flower in the higher orders of plants, we observe also that certain numbers prevail, but they are less constant. In those which are called monocotyledonous, in which there is apparently one lobe in the seed, the three-ranked arrangement prevails, as in crocus, iris, tulip, &c. The four- and five-ranked, on the other hand, are most frequent among dicotyledonous plants. Fuchsia, epilobium, &c., have the whorls of the flower in groups of 4. In primroses, and many others, the number 5 prevails --- that is, the quinary; among them, however, there are some exceptions, the number 3 being seen in magnolia, barberry, &c.
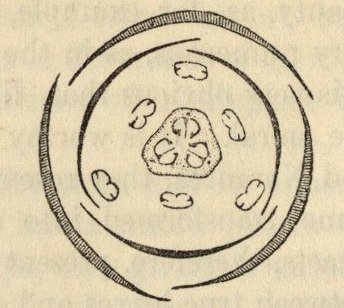
As an example of the three-ranked arrangement in the monocotyledonous division, we may take the flower of a hyacinth ; we observe on the outside 3 parts, or "sepals" as they are called, forming the "calyx" or cup. More internally, we see other 3 --- the petals --- the corolla, or coloured part of the flower. Next we find 6 "stamens" in two rows, an outer and inner, and in the centre of the flower a seed-vessel of 3 pieces conjoined; all these alternate with each other. The same succession of parts may be observed in complete flowers of dicotyledons, the numbers in each whorl being, however, mostly 4 or 5, although there are exceptions to this.
It seems to be a fair conclusion, from structures and arrangements here recorded, that in plants, whether high or low in the scale, certain principles regulate the number and arrangement of different organs, and that even in what is popularly considered to be "admirable confusion," the mighty "reign of law" prevails.

Photo by L. Shyamal, 2006.
It is perhaps easy to see why this approach attracted so few followers. Dickie (like most other writers on this subject in the 1800s) lumps together disparate phenomena which share only the quality of somehow involving number theory or geometry. Some of the examples, particularly those at the end, do not seem particularly mysterious or impressive, such as the tendency of roughly spherical cells to form tetrahedral clusters: surely any other shape would be much more surprising! The parts of the essay which do hint at a "reign of law" amid the "confusion" of the living world --- the amazing Fibonacci series; Mitchell's ability (minor arithmetic errors notwithstanding) to fit the shapes of leaves with fairly simple polynomials --- do not come through as forcefully as one might wish.
Biologists were for many years interested in phyllotaxis and similar ordering phenomena only because they were helpful in classification ("4 teeth in tetraphis; 8 in some species of orthotrichum"). The underlying "cause" was assumed to be random variation --- after all, anything with teeth is bound to have a certain number of them, and probably the same number as its close relatives!
Physicists, particularly in the Twentieth Century, had a strong aversion to "numerology", a word they used in a way peculiar to themselves. Even legendary figures like Dirac and Eddington were accused of "numerology" for suggesting a signal in the seemingly random digits of natural constants.
And so, the Mathematics of Plants has waited for a more sympathetic era to begin revealing itself. Perhaps for this era, perhaps not.

Fibonacci tree. [Drawing by "Profvk"]
LEVIATHAN: The War between Physics and Biology
- 2012 Oct. 22: Part 1: Introduction
- 2012 Oct. 29: Part 2: Cambridge as Jerusalem
- 2012 Nov. 26: Part 3: Go It, Charlie!
- 2013 Feb. 11: Part 4: Poetics -- It is Reasonable -- Someone Speaks
- 2013 Aug. 12: Part 5: The Mathematics of Plants
- To Be Continued ....