Net Advance of Physics: Courseware
The New Joly
Chapter I, Article 2.
Sum of two vectors. Commutative property.
- The sum obtained by adding the vector BC to AB
is denoted by BC + AB, and is defined to be the vector AC.
Thus symbolically (fig. 1),
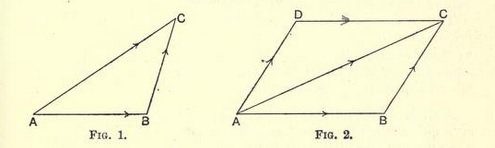
- Completing the parallelogram, ABCD, the definition of
addition gives likewise the equation (fig. 2)
DC + AD = AC
or
AB + BC = AC,
because the vectors DC and AD are respectively equal to AB and
BC. Thus the sum of two vectors is independent of the order in
which they are added, or the addition of two vectors is a
commutative operation.
- In certain systems of vector analysis, the word vector is used in
a different sense, and a vector cannot be determined without reference
to its position. In these systems, a vector is thought of as
bound to a point in space, viz. the point whence the
vector emanates. The commutative law is not obeyed by such bound vectors.
- Another example of non-commutative addition -- the addition of
great-circle arcs -- will be found in
Art. 21.

