PART 1D: Minkowski's words are in boldface.

"If we then take OC′ and OA′ as axes for parallel coordinates x′ and t′ with units OC′=1, OA′=1/c, then this branch of the hyperbola again has the equation
and the transition from x, y, z, t to x′, y′, z′, t′ is of the type under consideration."
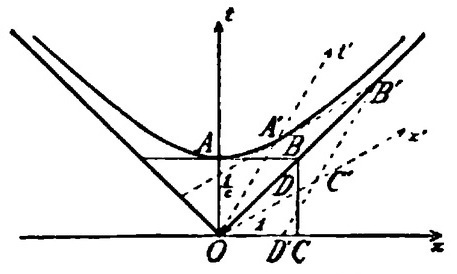
Consider first the ordinary, unprimed system: the familiar plane of elementary geometry, with its vertical axis arbitrarily labelled ct. Any point (x, ct) in the plane can be described by a vector r. If we call the unit vectors in the x and ct directions e and f respectively, we can write:
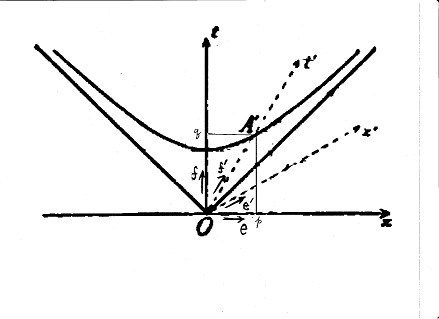
But we are not confined to using the particular axes x and y. We could use any two (non-parallel) lines intersecting at the origin and call them "axes". We could resolve r into components along these axes x′ and ct′ just as we could resolve it into components x and ct along the conventional Cartesian axes. We could define "basis vectors" along these axes: call them e′ and f′.
Obviously, a point's actual location does not change because we have measured it relative to a different set of axes: we can write for any arbitrary point:
Minkowski's e′ coordinate is a bit less easily described: he says it is directed along the tangent to the hyperbola at A′.
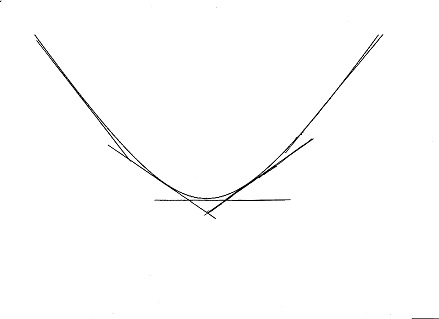
In the figure we see tangent lines to an hyperbola drawn at various points. Notice that at the far right, where both x and ct are very large and positive, they have slope 1, like the asymptote. At the far left, where x is a large negative number, but ct is again large and positive, the slope approaches −1. At the centre, where x is zero, the slope is also zero.
This might lead one to guess that the slope is x/ct. (The reader should verify that this expression has the right behaviour.) That is in fact the correct answer; readers who know calculus can obtain it by writing the equation for the hyperbola c²t² - x² = 1, solving for ct, and differentiating. At A′, therefore, the slope of the x′-axis is p/q.
Now the slope of a line is the tangent of the angle which it makes with the horizontal. This suggests that we choose the x-coordinate of e′ to be q/L, so the ct-coordinate will be q times the tangent of the angle, that is, qp/qL = p/L. So e′ = (q/L)e + (p/L)f.
We are almost at our destination. For any arbitrary point, we can write both primed and unprimed position-vectors, set them equal, and equate components:
Clearly different geometrical figures with known formulæ in terms of x and ct will have different, probably much more complicated, formulæ in the primed coordinates, which can be obtained from the standard forms by inserting the above expressions. Let us consider the case of the hyperbola c² t′² - x′² = 1.
So near and yet so far! This is certainly an hyperbola in the primed coordinates, but it is not quite the same hyperbola: the scale is wrong.
To remedy this, we simply define a new system of units -- "units OC′=1, OA′=1/c," according to Minkowski --- that is, units such that L = 1. We use these units only in the primed coordinate system; in effect, L is a "primed meter" used for measuring primed quantities. With these units:
Success!
TIME AND SPACE, by Hermann Minkowski