 Minkowski's Figure 2.
Minkowski's Figure 2.
PART 3A: Minkowski's words are in boldface.
 Minkowski's Figure 2.
Minkowski's Figure 2.
"Through the world-postulate a similar kind of treatment of the four determining elements x, y, z, t becomes possible. Through it, as I shall now show, we gain an insight into the forms under which physical laws operate. Above all, the conception of acceleration becomes sharply defined."
"I shall use a geometrical mode of expression which at once suggests itself, at the same time tacitly ignoring z in the triplet x, y, z. I take any world-point, O, as the space-time origin.
"The cone c² t² - x² - y² - z² = 0 with O as vertex consists of two parts, one with the values of t < 0 another with the values of t>0. The first, the past-cone of O consists, let us say, of all world-points which 'send light to O'."
For example, the stars (and all other objects) are seen "as they were in the past", when the light which we see now was emitted. Light travels at one light-year per year, so all the visible past lies along a (four-dimensional generalisation of a) cone in Minkowski space-time.
"The second, the 'future' cone of O, consists of all points which 'receive light from O'."
Future observers will see us as we are today when light from the here and now reaches them.
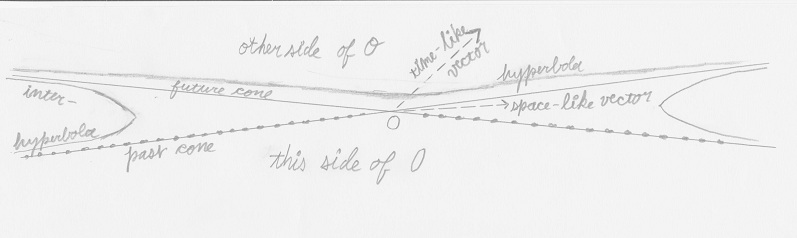
"The region bounded only by the past-cone of O may be designated this side of O, and that bounded only by the future-cone, the other side of O."
I have corrected Carus's translation, which is corrupt -- hardly surprising, since Minkowski uses the preposition nach in a very confusing way.
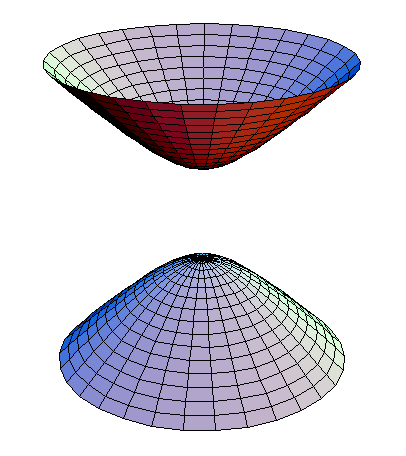
"The hyperboloid sheet considered above, F = c² t² - x² - y² - z² = 1, t > 0 falls on the other side of O."

"The region between the cones is filled with the hyperboloidic forms of one sheet
"If now in analogy to the concept of a vector in space, we call a directed tract in the manifold x, y, z, t, a vector, we must differentiate between time-like vectors with direction from O to the sheet +F=1, t>0, and space-like vectors with a direction from O to −F=1."
That is, time-like vectors lie inside the cones, where t² > x², and space-like vectors lie in the region outside the cones, where t² < x².
"The time-axis can be parallel to any vector of the first kind."
This is a key point. The time-axis can be any t′ with slope less than c, so that the square root of (1-(v/c)²)) is a real number. If this is not the case, measuring x′ intervals as in the previous blog-installment would produce an imaginary result, and that, presumably, would be absurd. And there is worse to come:
"Every world point between the past cone and future cone of O can be arranged by the system of reference to be simultaneous with O, but equally well as previous to O or later than O."
Hence the well-known association between faster-than-light motion (that is, motion in the region between the cones) and time travel. "Tachyons", as the inhabitants of the region between cones will be named in the Twentieth Century, do not obey the rule that cause must come before effect.
Why does causality fail between the cones? Consider the black and blue frames in the figure. In the black frame, A lies in the future; in the blue frame, it lies in the past.
"Every world-point on this side of O is necessarily always previous to O, every world-point on the other side of O necessarily always later than O.

"Passing the limit for c=∞ would correspond to the complete closing up of the wedge-shaped section between the cones into the plane manifold t=0. (In our figures this section has purposely been made of different widths.)"
If the speed of light is increased, a photon goes farther and farther in the horizontal direction for each second elapsed in the vertical direction. Therefore the cones become ever shallower and thus ever wider, while the "faster than light" region in between becomes shallower. In the Newtonian limit of infinite light-speed, the acausal realm of the tachyons disappears entirely.
TIME AND SPACE, by Hermann Minkowski