The Net Advance of Physics: Gamma-Ray Pulsar Emission Models, by Alice K. Harding -- Section 3A.

Polar Cap Models

Polar cap models divide according to the mechanism of

acceleration above the surface of the neutron star (see Usov 1996,

for more detailed review of acceleration mechanisms). In pulsars

having , where is the direction of the rotation axis, the

corotation charge ( ) above the magnetic poles is

negative. If the neutron star surface temperature, K

where is the electron surface binding temperature, then electrons

are freely released from the surface to be accelerated in parallel

electric fields induced by space-charge-limited flow (Michel 1991),

field-line curvature (Arons & Scharlemann 1979, Arons 1983)

and inertial frame dragging (Muslimov & Tsygan 1992). In these

models, at the surface and increases with height.

In pulsars having , the corotation charge above the poles

is positive and if K, where is the ion surface binding

temperature, then the ions are trapped in the surface. Since the

corotation charge cannot be supplied, a vacuum gap and thus a

non-zero grows at the stellar surface (Ruderman & Sutherland

1975). In most cases, the is shorted out at some altitude by the

onset of electron-positron pair cascades in the strong magnetic

field. However, the creation of bound-pairs (Shabad & Usov 1985)

instead of free-pairs in fields could delay the shorting

out of to larger heights above the surface, thus increasing the

acceleration energy. But Usov & Melrose (1995) found this to be an

important effect only in Ruderman-Sutherland type models.

Several different kinds of models for polar cap pair cascades have

been studied. If the accelerated primary particles reach energies of

, then curvature radiation will dominate their energy loss.

For inverse Compton scattering of X-rays, either

non-thermal cascade emission or thermal emission from a hot

polar cap, will be more important. More specifically, the energy loss

for curvature radiation of an electron moving parallel to a

magnetic field with radius of curvature cm will exceed

the energy loss due to non-magnetic inverse Compton scattering of

blackbody radiation at temperature K, when

(valid for in fields around G,

Dermer 1990).

At , resonant Compton scattering will be

important because the soft photons at temperatures near K

will be blueshifted into the cyclotron resonance in the electron rest

frame, greatly enhancing the scattering cross section and thus the

energy loss rate (Daugherty & Harding 1989, Dermer 1989). The

accelerated particles will radiate -rays by curvature radiation,

inverse Compton scattering (or a combination of both) which then

pair produce by the process in the strong magnetic field.

The pairs are produced in excited Landau states which decay by

emission of synchrotron photons, many of which will also produce

pairs. The cascade will continue, reprocessing and thus softening the

primary emission spectrum, until the photons escape.

 
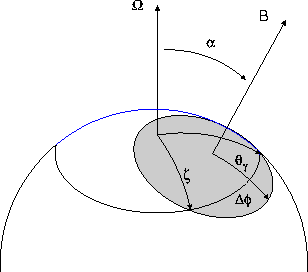
Figure 1: Geometry of single polar cap (SPC) emission. is the observer polar angle.

Although it is possible for emission from both polar caps to be

visible to observers in the proper orientation, these models have

focussed in the last few years on emission from a single polar cap

(SPC). In both the curvature radiation-induced pair cascade

(CRPC) and the Inverse Compton-induced pair cascade (ICPC)

models, the -ray emission pattern is a hollow cone. Since the

radius of curvature of the magnetic field lines is infinite at the poles

and decreases towards the polar cap rim, the curvature emission is a

maximum at the rim in the CRPC models. In the ICPC models, the

emission is also maximum at the rim where the angle between the

relativistic particles moving along field lines and the soft photons is

largest. The -ray beam half-angle, , is determined

approximately by the locus of the tangents to the outermost open

field lines:

where is the polar cap half-angle, r is the radius of emission

and R is the neutron star radius. When as shown in Figure 1,

an observer may see a broad double-peaked -ray pulse profile,

with bridge emission from inside the polar cap rim. In CRPC models

one can allow for extended acceleration regions (up to several

stellar radii) above the polar cap, and the outward flaring of

the field lines with height rapidly increases to as large as to

(Daugherty & Harding 1996, hereafter DH96). Thus, CRPC models

no longer require very small inclinations to accommodate large

phase separations in doubly-peaked profiles, as in previous SPC

models (Daugherty & Harding 1994; Sturner et al. 1995, Sturner et

al. 1995). Figure 2 shows simulated distibutions of double pulse peak

separations, , expected for random observers and various

assumed distributions of pulsar obliquity. For uniform , the

distributions predict enough large phase separations only for very

large , and are then too sharply peaked to allow many small

values of . But when is limited to even moderately small

values, the predicted distributions are more consistent with those

observed and will allow smaller values of .

 
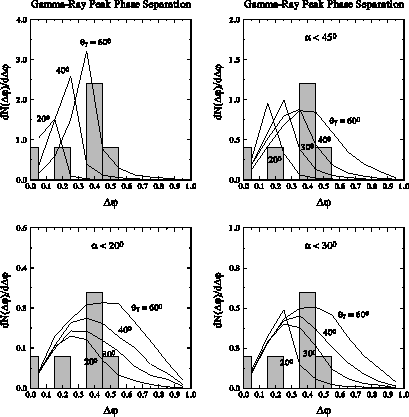
Figure 2: Simulated (solid lines) and observed (shaded histogram) distributions of pulse peak separation, for uniform (upper left) and limited obliquity .

 
• Curvature radiation induced pair cascades
• Inverse-Compton induced pair cascades

BIBLIOGRAPHY