
In the early 1980's, researchers such as Benioff, Bennett, Deutsch, Feynman and Landauer studied the possibility of performing computations using the principles of quantum mechanics, and conjectured that a machine based on these principles might be able to solve certain types of problems more asymptotically more rapidly than can be done on a conventional von Neumann computer. This study remained purely academic until the early 1990's, when Lloyd proposed that such a quantum computer might be built from an array of coupled two-state quantum systems, each of which can store one quantum bit, or qubit, of information. Shortly thereafter, Shor proved that a quantum computer would be capable of factorizing integers in polynomial time, thereby showing that the exponential number of degrees of freedom accessible to a quantum computer does indeed enable it to solve some problems more efficiently than is believed possible on a conventional machine.
Also in the early 1990's, Adleman and Lipton demonstrated that the massive number of degrees of freedom in a macroscopic ensemble of molecules, in conjunction with the specificity of DNA biotechnology, can also be used to solve difficult combinatorial problems. Because the number of degrees of freedom increases only linearly with the size of the system, however, DNA computing does not appear to be capable of altering the actual complexity of a problem. In this sense a DNA computer is simply a (very) massively parallel conventional computer. Other problems associated with DNA computing include the need for laborious wet chemistry, in order to perform the computations and extract the results, and the lack of a general methodology for automatically setting up and carrying out such computations. DNA computing nevertheless has one big advantage over quantum computing: While no one has yet built a true quantum computer able to handle more than two or three qubits, small DNA computations can be readily performed on macroscopic samples under ambient conditions.
A few years ago, it was found that nuclear magnetic resonance, or NMR, spectroscopy provides a means of combining many of the best features of DNA and quantum computing. In particular, an NMR computer can be programmed electronically just like a quantum computer in principle could be, but at least small prototypes can be implemented using macroscopic liquid samples much as in DNA computing. The main difference between an NMR computer and a quantum computer is that one does not get wave function collapse to a random observation on performing a measurement in NMR spectroscopy, but rather ensemble averaging over the distribution of microscopic observations. We have shown that this effect enables one to trade exponential growth in the computational time required for an exponential increase in the sample size needed, just as can be done in DNA computing. It does not, however, limit the potential for asymptotic reductions in the time required to solve those problems for which good quantum algorithms are available.
In the following introduction, we shall assume the reader is familar with the basics of atomic and molecular physics, and has an elementary knowledge of quantum computing. Several excellent introductions to the latter are available on the web; we would recommend in particular Braunstein's tutorial. Those who are ready for a more advanced accounts of ensemble quantum computing may wish to skip directly to the documents linked in the Further Information section.
The local field strength at each atom of a molecule is modulated by its electronic environment, resulting in slightly different Larmor frequencies even for nuclei of the same isotope; this is called the chemical shift. If in addition an RF (radio-frequency) field is applied perpendicular to the static field at the shifted Larmor frequency, the spins nutate (turn) about the RF field vector, resulting in a quantum superposition of their up and down states. The spins can also interact in one of two ways: First, there is a through-space dipole-dipole interaction, which depends on both the longitudinal (i.e. along the field) component as well as on the relative phases of the spins. Second, there is a through-bond J-coupling, which is mediated by electron correlation in the chemical bonds of the molecule. These nonlinear interactions enable the selective manipulation of the state of one spin, depending on the states of its coupled partners.
In order to describe a macroscopic ensemble of spins, one must use the density matrix formulation of quantum statistical mechanics. If N ~ 1022 is the number of spins in the sample, this is a trace one Hermitian matrix of order 2N. In a liquid, the dipole-dipole interactions between the spins in different molecules are averaged to zero by the rapid diffusion of the molecules about one another. This together with the indistinguishability of different molecules of the same chemical species enables us to use a reduced density matrix of order 2n, where n << N is the number of spins in one molecule. This reduced density matrix is obtained as the ensemble average over the density matrices of the individual molecules, i.e. by tracing the full density matrix over all the molecules of the sample but one, and then averaging over all choices of this one molecule. The reduced density matrix likewise evolves under the Liouville-von Neumann equation, and yields ensemble average observables via the trace product.
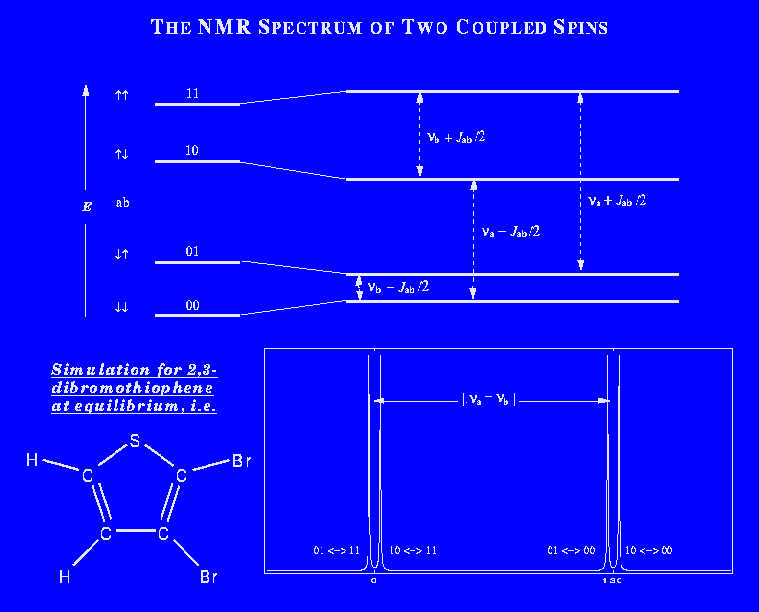
Because the interaction of the spins with the field is small compared to kT, NMR samples at ordinary temperatures are only weakly polarized, which means that the reduced density matrix is very close to the identity matrix. The difference from the identity undergoes unitary evolution in the presence of a transverse RF field, such that the dipole expectation values nutate as described above. To measure the usual one-dimensional NMR spectrum of a sample at equilibrium, one applies an RF pulse which nutates these expectation values to the plane transverse to the static field, where they subsequently precess in phase to produce a net rotating magnetic moment and hence a signal in the receiver. The spectrum obtained by Fourier transformation of this signal is related to the properties of the spin states as follows:
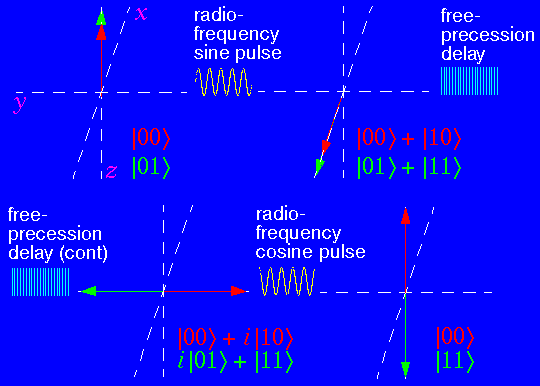
To illustrate how this is done, let us consider the quantum XOR (or controlled NOT) gate implementation shown in the Figure at the very top of this web page. Following the common practice in NMR spectroscopy, we shall now use the word "spin" to refer to an ensemble of chemically equivalent single spins, each in a different molecule of the sample. We can then say that this implementation of the XOR gate consists of a selective sine-pulse, which nutates the magnetization due to the "first" spin into the transverse plane, followed by a delay of half the inverse coupling (in Hz.), and then an equal cosine-pulse also selective for the first spin. This is known in NMR as the INEPT pulse sequence. In the figure, the two vectors correspond to the magnetization due to the first spin in those molecules in which the second spin is up (green) and down (red). The spinors corresponding to each of these states are shown below each vector diagram.
Through the effect of J-coupling, the first spin is subject to slightly different magnetic fields in these two populations of molecules, and so precesses at slightly different rates in each. After a period of 1/(2J), the spin points in exactly opposite directions in each population, and hence when the final cosine-pulse realigns it with the field the spin has been flipped in those molecules wherein the second spin was "up". If we regard spin down as a "0" and spin up as a "1", this corresponds exactly to replacing the state of the first spin with the result of its XOR with the second. Up to phase factors, the net unitary matrix, and its effect on the basis spinors, is:
/ 1 0 0 0 \ |00> \ |00> | 0 0 0 1 | . |01> -----\ |11> | 0 0 1 0 | . |10> -----/ |10> \ 0 1 0 0 / |11> / |01>
The primary difference between a quantum computer and an ensemble quantum computer lies in the fact that, as explained above, a measurement on an ensemble quantum computer yields the expectation value of the observable, rather than a random eigenvalue thereof. If interference effects can be used to concentrate the coherence in a single state, of course, these two types of measurements will yield the same result. In the general case, the measurement of an expectation value can reveal the presence of a "significantly populated" state in a superposition with a single measurement (subject to signal-to-noise considerations), whereas many repetitions of the calculation and measurement would be required on a quantum computer before the wave function collapsed into the state of interest. In principle this permits a large, though (for a fixed sample size) constant factor, reduction in the time required over what might be required for the same computation on a quantum computer. Via Fourier transform techniques, an NMR implementation of an ensemble quantum computer is also able to simultaneously measure many expectation values in the single spectrum.
The primary problem with emulating a quantum computer using pseudo-pure states is that the population of any single state in thermal equilibrium falls off exponentially as the number of spins n in the molecule increases. Thus our present methods of preparing pseudo-pure states from thermal equilibrium states by averaging all but one of the populations to equality results in an exponentially decreasing the signal-to-noise in the corresponding spectrum. Although this limits the size of the quantum computer that can be emulated by such a preparation to ca. 8 to 10 spins, this is already considerably more than has been reached by any approach that requires a perfectly isolated quantum system. Moreover, the field of ensemble quantum computing is still in its infancy, and it is an open question if our present methods of preparing pseudo-pure states are the only ones possible, or for that matter if pseudo-pure states are really needed in order to carry out computationally interesting procedures on ensembles of quantum systems.
In the popular press, there has been a good deal of confusion over the purpose of research into physical implementations of nonstandard models of computation. While the possibility exists that such research may someday lead to commercial hardware capable of computations beyond the reach of any conceivable computer based on today's VLSI technologies, this is neither certain nor at all likely in the near future. As we see it, the immediate goals of the field are two-fold: