3.26 Space-time
Poisson process
Consider a highway that starts at x = 0 and extends
infinitely eastward toward
increasing values of x. Automobile accidents and breakdowns
occur along the
highway in a Poisson manner in time and space at a rate y per hour
per mile. Any accident
or breakdown that occurs remains at the location of occurrence until
serviced.
At time t = 0, when there are no
unserviced accidents or
breakdowns on the highway, a helicopter starts
from x = 0 flying
eastward above the highway at a constant speed s. As a
service unit, the
helicopter will land at the site of any accident or breakdown that
it flies over.
Moreover, given at time t the helicopter is located at x =
st, the helicopter can
be dispatched (by radio) to service any accident or breakdown that
occurs behind it (i.e.,
at values of x  st). We assume that any such
dispatch occurs
immediately after the accident or breakdown occurs. st). We assume that any such
dispatch occurs
immediately after the accident or breakdown occurs.
We are interested in the time the helicopter
first becomes busy, either
by landing at an accident/breakdown site or by being dispatched to
an accident/breakdown
behind its current position; in the latter case, the instant of
dispatch (not the time of
arrival at the scene) is the time of interest.
Let
T = time that the helicopter first becomes busy
a.
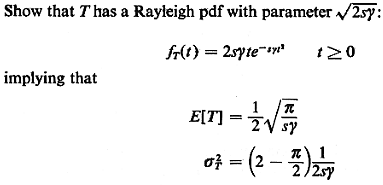
b. Let
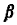  probability that the first
accident/breakdown is a dispatch
incident behind the helicopter probability that the first
accident/breakdown is a dispatch
incident behind the helicopter
1 - 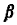  probability that the first
accident/breakdown occurs as a
result of patrol (i.e., the helicopter
discovers it) probability that the first
accident/breakdown occurs as a
result of patrol (i.e., the helicopter
discovers it)
Show that 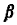 = 1 - = 1 - 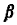 = 1/2. = 1/2.
Hint: Condition on the event that the first
accident breakdown occurs in
the time interval (t, t + dt).
c. Let
X  location of the first
accident/breakdown that the
helicopter services location of the first
accident/breakdown that the
helicopter services
Show that
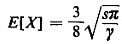
d. Suppose that
L1, =
time of first
accident/breakdown that the helicopter flies over, assuming that
it is no longer
dispatched by radio (i.e., all incidents are
helicopter-discovered incidents)
L2 = time of first
accident/breakdown that the
helicopter is dispatched to, assuming that it never services
accident/breakdowns that it
flies over
Then, for instance, T =
Min[L1,
L2].
Show that L1 and
L2
are identically distributed Rayleigh random variables, each with
parameter 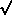 sy.
Finally, argue that L1
and L2
are independent, thereby concluding that the minimum of two
independent Rayleigh random
variables, each with parameter sy.
Finally, argue that L1
and L2
are independent, thereby concluding that the minimum of two
independent Rayleigh random
variables, each with parameter 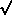 y, is itself a Rayleigh random
variable with
parameter y, is itself a Rayleigh random
variable with
parameter 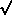 2y. 2y.
3.27 Circular city,
revisited Suppose
that two points (R1,  2)
and (R2, 2)
and (R2,  2) are
independently, uniformly distributed over a circular city of radius
ro
and area A= 2) are
independently, uniformly distributed over a circular city of radius
ro
and area A= 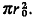 Suppose further that this city has a
large number of radial
routes and circular ring routes so that the travel distance between
(R1, Suppose further that this city has a
large number of radial
routes and circular ring routes so that the travel distance between
(R1,
 1)
and (R2, 1)
and (R2,  2) can be
accurately approximated as 2) can be
accurately approximated as
D = |R1 - R2| + Min [ R1, R2] | 1
- 1
-  2| 2|
where 0  | | 1 - 1 -  2| 2|
  signifies
the magnitude of the angular difference between signifies
the magnitude of the angular difference between  1
and 1
and  2. In words,
travel from an outer point, say,
(R1, 2. In words,
travel from an outer point, say,
(R1, 1)
if R, > R2, to an inner point
(R2, 1)
if R, > R2, to an inner point
(R2, 1)
first occurs along a radial route to a ring located a distance R2
from the city center,
and then along that ring (in the direction of minimum travel
distance) to (R2, 1)
first occurs along a radial route to a ring located a distance R2
from the city center,
and then along that ring (in the direction of minimum travel
distance) to (R2, 1);
the same path is traveled in reverse if travel is from
(R2, 1);
the same path is traveled in reverse if travel is from
(R2, 1)
to (R1, 1)
to (R1, 1).
A sample path is shown in Figure P3.27. 1).
A sample path is shown in Figure P3.27.
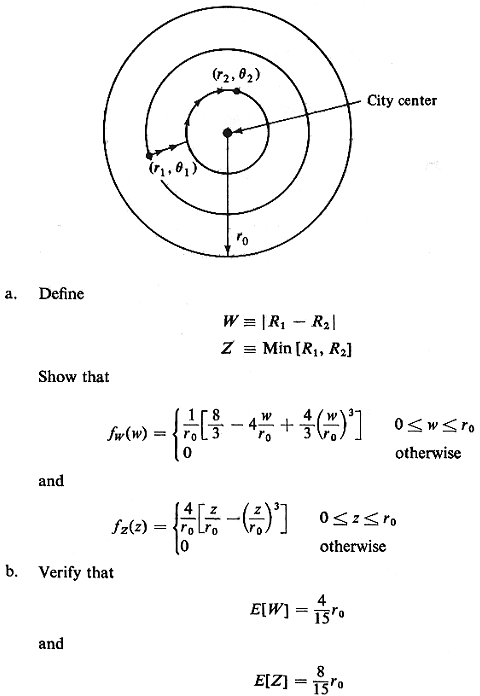
and thus
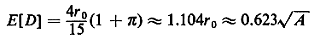
Compare this result to analogous results in
Problems 3.20 and 3.21.
3.28 Circular city, revisited
again Suppose we
modify the previous example so that travel from the outer point to
the inner point, when
it reaches the inner circle (say of radius
R2 if R2
< R1), proceeds from that point either
along an arc
of radius R2 (as in Problem 3.27) or
through the city center
along two radial routes directly to the possiblities are shown in
Figure P3.28.

3.29 Effect of traffic lights on
travel times A
vehicle travels a route from a to b, incurring a total travel
time
T = 6 +
W1 +
W2
(minutes)
where 6 = time to traverse
the distance (at
constant speed) from a to b
W1
= delay incurred at traffic ight 1
W2
= delay incurred at traffic light 2
As shown in Figure P3.29, the route is partitioned
into three 2-minute
travel-time segments. Each traffic light operates on a fixed cycle
of 1 minute green,
followed by I minute red. (We assume that no time is wasted in
decelerating and
accelerating, should one or two lights cause the vehicle to stop.)

Suppose that exactly at some prespecified time (say
12: 00 noon) we
examine the "phase"  i, of each traffic
light (i = 1, 2). By definition, i, of each traffic
light (i = 1, 2). By definition,
 i = time until
light
i next turns to green (0 i = time until
light
i next turns to green (0   i < 2) i < 2)
For each light, we suppose that  i,
is independently, uniformly distributed over [0, 2]. However,
once i,
is independently, uniformly distributed over [0, 2]. However,
once  i
is known, its value isfixedfor all time. i
is known, its value isfixedfor all time.
Throughout this problem, we assume that departure
times at a occur
independently of the phases of the traffic lights.
a. Find the mean and variance of the travel time
from a to b.
b. Find the probability density function of the
travel time from a to b.
c. Let k = number of traffic lights at which the
vehicle is delayed. Find
the z-transform of the probability mass function for k.
For parts (d) and (e), only [not for parts (f)-(h)],
let
C = event that for the most recent vehicle
traveling from a to b, the
vehicle was stopped only at traffic light 1
d. Find the conditional joint probability density
function for  1
and 1
and  2,
given C. 2,
given C.
e. Find the conditional probability density
function for the travel time
from a to b for the next vehicle to travel from a to b, given C.
(Assume that you know
nothing about when the next vehicle will leave a.)
For parts (f)-(h), suppose that vehicles leave a in
a Poisson manner with
mean 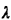 = 1 vehicle per minute. Vehicles occupy zero space and, when
in a traffic light
queue, accelerate and decelerate instantaneously together.
= 1 vehicle per minute. Vehicles occupy zero space and, when
in a traffic light
queue, accelerate and decelerate instantaneously together.
f. Is the vehicle arrival process at b a
Poisson process? Why or
why not?
g. Determine the mean and variance of the queue
length (number of
vehicles) at traffic light I at the instant before the light turns
green. (This is a
primer for Chapter 4.)
h. A traffic engineer adjusts the phases of the
two traflac lights so that
 1
= 1
=  2
= 0 (relative to 12: 00 noon). Suppose that at 12: 00 noon we are
given conditional
information that no vehicles have left a during the last
8 minutes. Carefully
sketch and label the probability density function for the time of
arrival at b of the next
vehicle to arrive there. 2
= 0 (relative to 12: 00 noon). Suppose that at 12: 00 noon we are
given conditional
information that no vehicles have left a during the last
8 minutes. Carefully
sketch and label the probability density function for the time of
arrival at b of the next
vehicle to arrive there.
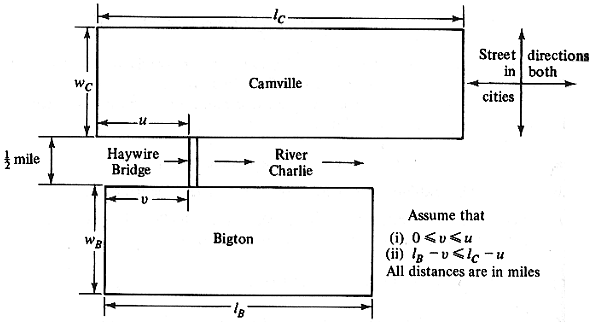
3.30 Expected travel distances
in a two-city area
Consider the cities of Camville and Bigton, which are separated by
the River Charlie. Only
the 1-mile-long Haywire Bridge connects the two towns. The layout of
the cities is shown
in Figure P3.30. The population of each of the two cities is
uniformly distributed
throughout the cities. Camville has a density of 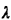 c people per
square mile; Bigton's
density is c people per
square mile; Bigton's
density is 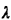 b people per square
mile. b people per square
mile.
a. Find the expected travel distance between two
randomly selected people
in Camville; find the expected distance between two randomly
selected people in Bigton.
b. Find the expected distance between a randomly
selected person in
Camville and a randomly selected person in Bigton.
C. Find the expected distance between two randomly
selected people in the
greater Camville-Bigton metropolitan area.
d. Find the expected distance between two randomly
selected people, one
from each town, assuming that one can cross the River Charlie at
any point along
the 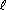 B
miles of Bigton that run along the river. By how much does your
answer differ from your
answer in part (b) ? B
miles of Bigton that run along the river. By how much does your
answer differ from your
answer in part (b) ?
e. Compute numerical values for all the
questions above assuming that
i. 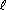 B
= 4 miles
ii. B
= 4 miles
ii. 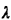 B
= 2,000 people/square mile B
= 2,000 people/square mile
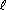 c
= 6 miles c
= 6 miles
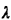 c
= 1,000 peoplel/square mile c
= 1,000 peoplel/square mile
u = 2 miles
v = I mile
WB = 5 miles
Wc = 3 miles
3.31 Assigning commuters to
subway stations
Figure P3.31 shows an urban area which is served only by a
mass-transit rail line with
four stops ~A, B, C, and D) as shown. There is a single destination
at point T for all
trips generated from this area (assume that all trips go exactly to
point T) during each
day's morning rush hour.
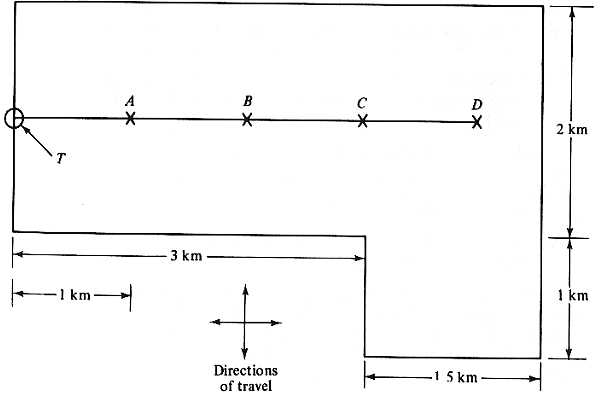
In order to get to a transit line
station or to walk
directly to T, the residents of the area must walk on an
"infinitely dense" grid
of urban streets whose directions run parallel to the boundaries of
the area.
The following information is now given:
1. During the morning rush hour the area generates
200 trips per km^2 with
trip origins distributed uniformly.
2. Headways between trains are constant and equal
to 6 minutes, and each
train rider is equally likely to arrive at a station at any time
between two successive
departures of trains from that station. (All riders are assumed to
be able to ride on the
first train to leave a station after their arrival there.) Stops
at each station are I
minute long.
3. Trains travel between stations at a speed of 30
km/hr (this includes an
adjustment for acceleration and deceleration periods). People walk
at a constant speed of
5 km/hr.
4. The sole criterion that each individual uses to
determine his/her route
is to minimize the expected total trip time to T (including time
spent waiting for and
riding on trains). Each individual is assumed to know all the
information given above
concerning travel speeds, headways, and so on.
a. Determine the number of riders who will be
using each of stations A, B,
C, and D each day, as well as the number of those that will be
walking directly to T.
b. Compute the expected travel time for a random
resident of this area
each day.
c. Draw the boundary of the region whose residents
are 9 minutes or less
away from T. Repeat for the 20-minute boundary. (Be careful in
your work.)
d. Repeat part (a) by making the change in the
initial data indicated
below, while keeping everything else the same as before. (Each
part below is separate.)
1 . The train speed increases to 40 km/hr.
2. Train headways are increased to 10 minutes.
3. Train speed >> walking speed.
e. Repeat part (a) by assuming that headways
between trains are described
by a negative exponential pdf with a mean of 6 minutes.
3.32 Optimal district design in
terms of city blocks
In this problem we shall examine the question of optimal district
design for cases in
which the dimensions of a district can assume only integer values
due to the grid
structure of streets.
Consider again the case described in Problem
3.15, which involved an n
x m rectangular grid district with two-way streets. In
that problem you have
shown that
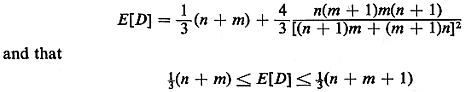
Suppose now that we wish to
design a district so as to
minimize E[D], subject to the constraint that the area of the
district is greater than or
equal to some value A (i.e., mn 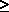 A). (It is not reasonable to set an
equality constraint since m
and n can take only integer values.) For instance, if A = 44, we
wish to find n and m such
that E[D] is minimized and the district contains at least 44 city
blocks. A). (It is not reasonable to set an
equality constraint since m
and n can take only integer values.) For instance, if A = 44, we
wish to find n and m such
that E[D] is minimized and the district contains at least 44 city
blocks.
a. Consider the quantity
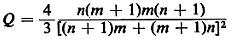
under the constraint n + m = C (where C is a
positive integer constant).
Argue that under this constraint Q is maximized when n = m (if C
is an even number) or n =
m + I (if C is an odd number), and minimized when n = 0 or when m
= 0.
Hint: Q is symmetric in n and m.
b. Show that the following algorithm will give the
optimal district
dimensions [LARS 72a]:
STEP 1: Set i = [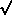 A], where [x] = smallest integer greater
than or equal to x. A], where [x] = smallest integer greater
than or equal to x.
STEP 2: Set j = i - 1 if i(i - 1) 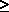 A; otherwise, set j = i. A; otherwise, set j = i.
STEP 3: Set k = i + 1, 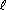 = j - 1. = j - 1.
STEP 4: If kt 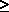 A, set i = k, j = 1; return to Step 3.
Otherwise, stop; the
optimal district dimensions are n = i, A, set i = k, j = 1; return to Step 3.
Otherwise, stop; the
optimal district dimensions are n = i,
m = j.
c. Apply your algorithm to find the optimal
district dimensions for the
case A = 44.
d. Compare numerically E[D] for the cases: m = 7,
n = 7; m = 6, n = 8; m =
5, n = 9; m = 4, n = 11. (All these designs satisfy mn 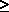 44.) What do you conclude
from these numerical
comparisons? 44.) What do you conclude
from these numerical
comparisons?
|