4.3 DEFINING THE QUANTITIES OF INTEREST
In this section we define the quantities and introduce the notation
that will be used in the rest of the chapter. We do this by focusing on a specific
queueing system and beginning to count at some instant t = 0 the number of users who
arrive at the system.
Let us concentrate on the ith user to arrive at that system after we
begin our counting process. Three important "events" can be identified with
respect to this ith user: the arrival of the user at the queueing system, the beginning of
service to the user, and the completion of service to the user. We shall denote the
instants when these three events occur as ta(i), tb(i), and tc(i),
respectively (with a standing for "arrival," b for "beginning" of
service, and c for "completion" of service).
We can now define the following quantities:
x(i)  ta(i)
- ta(i - 1) = ith interarrival time ta(i)
- ta(i - 1) = ith interarrival time
s(i)  ta(i)
- ta(i) = service time for the ith (in terms of order of arrival to the system)
user ta(i)
- ta(i) = service time for the ith (in terms of order of arrival to the system)
user
Wq(i)  tb(i)
- ta(i) = waiting time in the queue for the ith user tb(i)
- ta(i) = waiting time in the queue for the ith user
W(i)  tc(i)
- ta(i) = total time spent in the queueing system by the ith user ("system
occupancy time") tc(i)
- ta(i) = total time spent in the queueing system by the ith user ("system
occupancy time")
Obviously, from the foregoing definitions we also have
W(i) = Wq(i) + s(i) (4.1)
In general, the interarrival and service times are random variables, X(i) and S(i),
with pdf's fX(i)(x) and fS(t)(s), respectively.
[The use of the term "probability density function" is made here in a general
sense. The random variables X(i) and S(i), i = 1, 2, 3... can be discrete, continuous, or
mixed.]
We shall assume from now on that, unless otherwise stated, the interarrival-time random
variables X(i) are independent and identically distributed [i.e., fX(1)(x) = fX(2)(x)
= ... = fX(x)]. Similarly, we shall assume that the service times S(i) are
independent and identically distributed with fS(1)(s) = fS(2)(s) =
... = fS(s). The expected values of random variables X and S appear so
frequently in the analysis of queueing systems that special symbols have been adopted for
them:
(1/  ) )  E[X]
(4.2) E[X]
(4.2)
(1/ ) )  E[X]
(4.3) E[X]
(4.3)
In words,  represents the expected number (or the "rate") of user arrivals at
the queueing system per unit of time. Similarly, ju is the expected number of service
completions per unit of time when a server is working continuously. Note that when all m
parallel and identical servers in a queueing system are working simultaneously, the rate
of service completions is equal to mp. represents the expected number (or the "rate") of user arrivals at
the queueing system per unit of time. Similarly, ju is the expected number of service
completions per unit of time when a server is working continuously. Note that when all m
parallel and identical servers in a queueing system are working simultaneously, the rate
of service completions is equal to mp.
Now if the queueing system is allowed to operate for a long time, it
can be expected, under certain conditions, to reach an equilibrium ("steady
state"). Without specifying what these conditions are, it is reasonable to assume
that the system occupancy times, w(i), and waiting times, wq(i), for large
values of i, will tend to become samples of two random variables W and W, respectively,
whose pdf's fW(w) and fq w(Wq) are independent
of the order, i, of a user's arrival. We shall refer to fw(w) and fW
q(wq) as the steadystate probability density functions for the
system occupancy times and the waiting times of users, respectively. We shall then define
the quantities
  E[W] = E[W] = 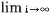 E[W[i]] E[W[i]] |
= expected system occupancy time
for a user under steady-state conditions |
 q q  E[Wq] = E[Wq] = 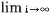 E[Wq[i]] E[Wq[i]] |
= expected waiting time in queue for a user
under steady-state conditions |
Rather than focus on user-related events at the queueing system [such as the ta(i),
tb(i), tc(i), etc.], we also could have looked at the system at
random points in time and defined the quantities
N (t)  total number
of users (including those in service) who are in the queueing system at time t total number
of users (including those in service) who are in the queueing system at time t
Nq(t)  number of users waiting in the queue at time t
number of users waiting in the queue at time t
For large values of t and under the (yet unspecified) proper conditions, we can expect
the distributions of variables N(t) and N,(t) to approach equilibrium (steady-state) pmf's
pN(n) and pNq(n).
We shall then use the symboIs

We shall also define here the quantity

From the definition of the utilization ratio (the reason for its name will become
obvious later), it is clear that, for a single-server queueing system,

whereas for a m-server queueing system,
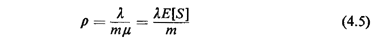
1 The use of the term "probability density function" is
made here in a general sense. The random variables X(i) and S(i), i = 1,2,3, ... can be
discrete, continuous, or mixed.
|