4.4 SOME IMPORTANT RELATIONSHIPS IN QUEUEING THEORY
We mentioned in Section 4.1 that queueing theory has been highly successful in deriving
expressions for the low moments of quantities such as the waiting times of the users of a
queueing system or the number of users present in the system at a given time. We shall now
begin our discussion with the derivation of a few important relationships involving the
expected values of these quantities,  , ,  q, q,  , and , and  q for a very general queueing
system. J. D. C. Little [LITT 611 is generally credited with being the first to prove
these relationships formally. Subsequent authors have shown that Little's results are
valid for queueing systems more general than he assumed in his original work [STID 74].
Here we shall use an informal and intuitive argument paralleling the one offered by
Kleinrock [KLEI 75]. q for a very general queueing
system. J. D. C. Little [LITT 611 is generally credited with being the first to prove
these relationships formally. Subsequent authors have shown that Little's results are
valid for queueing systems more general than he assumed in his original work [STID 74].
Here we shall use an informal and intuitive argument paralleling the one offered by
Kleinrock [KLEI 75].
The search for the relationships is motivated by the intuition-satisfying notion that
the average length of the queue in front of a facility offers a good indication of the
average waiting time for use of that facility (and vice versa). These relationships turn
out to be especially simple.
First, we shall position ourselves at the "entrance" of a queueing system and
count the number of users that arrive there during an interval of arbitrary length,  , beginning at the time t = 0 when
the system is empty (see also Figure 4.3). We let , beginning at the time t = 0 when
the system is empty (see also Figure 4.3). We let
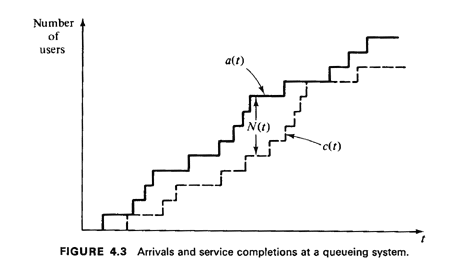
a( ) )  number of arrivals at the queueing
system in [0, number of arrivals at the queueing
system in [0, ] ]
Next, we count the number of users leaving the system at its "exit" and let
c( ) )  number of service completions in [0, number of service completions in [0, ] ]
If the system is empty at t = 0, the number of users in the system at the time t =  is given by is given by
N( )
= a( )
= a( ) - c( ) - c( )
(4.6) )
(4.6)
We can now use (4.6) to express the total amount of time, l( ), spent by all users in the queueing system
during the interval [0, ), spent by all users in the queueing system
during the interval [0, l. We
have l. We
have
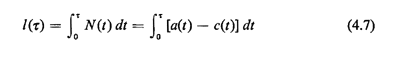
Clearly, 1( ) represents the
area between the functions a( ) represents the
area between the functions a( )
and c( )
and c( ), as illustrated in
Figure 4.3. ), as illustrated in
Figure 4.3.
The average number of users 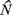 ( ( ) in the queueing
system during the interval [0, ) in the queueing
system during the interval [0,  ]
can now be obtained by dividing the total amount of time spent by all users in the
queueing system, l( ]
can now be obtained by dividing the total amount of time spent by all users in the
queueing system, l( ), by the
time ), by the
time  : :
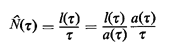 (4.8)
(4.8)
We have written (4.8) in this form because both ratios on its right-hand
side have very real physical meaning. The ratio a( )/ )/ is
simply the average number of arrivals per unit of time (the arrival rate) during the
interval is
simply the average number of arrivals per unit of time (the arrival rate) during the
interval  and can be
indicated, given our earlier notation, as and can be
indicated, given our earlier notation, as 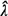  .
Similarly, l( .
Similarly, l( )/a( )/a( ) is the average time spent by a
user in the queueing system during the interval [0, ) is the average time spent by a
user in the queueing system during the interval [0,  ] and can be indicated, given our earlier notation, as ] and can be indicated, given our earlier notation, as 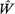  . We can then write . We can then write
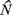 ( ( ) = ) = 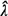   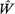  (4.9)
(4.9)
If we now let the length of the interval,  , tend to infinity, it is clear from our
earlier definitions of , tend to infinity, it is clear from our
earlier definitions of  , ,  , and , and  that these quantities represent the limits
of that these quantities represent the limits
of 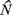 ( ( ) ) 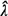  ,
and ,
and 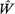  respectively. So if the limits of the
last two quantities ( respectively. So if the limits of the
last two quantities (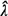  , and , and 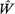  ) actually exist, the limit of ) actually exist, the limit of 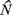 ( ( ) also exists and from (4.9) we have the relationship ) also exists and from (4.9) we have the relationship
 = =   (4.10)
(4.10)
This is one of the best-known results of queueing theory and is referred to as Little's
formula. Later in this chapter we shall explore the conditions under which the limits of 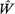  and of and of 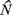 ( ( ) exist for many types of queueing systems. A few important remarks
are in order: ) exist for many types of queueing systems. A few important remarks
are in order:
In deriving (4.10), we stationed ourselves at the
"entrance" and "exits" of the queueing system. We could have performed
exactly the same analysis if we had counted entries to the queueing system (as before) but
exits from the queue (or, in other words, entries to the service facility). In that case
we would have derived the result
 q
= q
=   q
(4.11) q
(4.11)
where  q and q and  q are the average
number and average stay in the queue, as defined earlier. q are the average
number and average stay in the queue, as defined earlier.
In a similar way, but by focusing now on the service facility itself (i.e., by counting
entries and exits from the service facility), we could show that
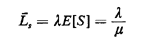 (4.12)
(4.12)
where  s, is the
(steady-state) average number of users in the service facility. [Note that this result is
independent of the number of servers, m. What matters on the right-hand side of (4.12) is
the average amount of time a user spends in the facility, E[S].] s, is the
(steady-state) average number of users in the service facility. [Note that this result is
independent of the number of servers, m. What matters on the right-hand side of (4.12) is
the average amount of time a user spends in the facility, E[S].]
In our discussion so far, we have never specified a queueing discipline. Thus, (4.
10) and (4.11) hold irrespective of the method used to determine the order of entry to the
service facility. [See also Section 4.9.] They also hold for the case where users belong
to a number of distinct classes to which difrerent levels of priority are assigned. Within
each of the classes, (4. 10) and (4.11) are valid.
The only condition that was placed on the arrival process at the queueing system is
that the quantity 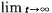 a( a( )/ )/  , the long-term arrival rate, be finite. To
appreciate the significance of this, consider a case in which the arrival rate, rather
than being a constant, is a function of some parameter-say, of the total number of users
present in the queueing system or of time. Then, we can still use (4.10) and (4.11), with
a value of , the long-term arrival rate, be finite. To
appreciate the significance of this, consider a case in which the arrival rate, rather
than being a constant, is a function of some parameter-say, of the total number of users
present in the queueing system or of time. Then, we can still use (4.10) and (4.11), with
a value of  equal to the
long-term average of the rate at which users enter the system. Similarly, for queueing
systems with finite queue capacity, for which there is the possibility that some potential
users will be turned away, we use (4. 10) and (4.11) with A equal to the average rate at
which users actually join the queueing system. We shall see several examples of this type
in subsequent sections. equal to the
long-term average of the rate at which users enter the system. Similarly, for queueing
systems with finite queue capacity, for which there is the possibility that some potential
users will be turned away, we use (4. 10) and (4.11) with A equal to the average rate at
which users actually join the queueing system. We shall see several examples of this type
in subsequent sections. A last relationship of importance which is always valid due to
(4.1) is
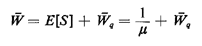 (4.13)
(4.13)
Note that (4.10), (4.11), and (4.13) make it possible, with given  and and  , to compute all four of the quantities , to compute all four of the quantities  , ,  q, q,  , and , and  q
if any one of them can be determined. q
if any one of them can be determined.
Finally, it is worth remembering the following convenient argument (not
"proof") that leads to (4.10) and (4.11). In the steady state, the average
number of users that a random user finds in a FCFS "system" upon arrival should
be equal to the number of users he or she leaves behind upon departure, with both of these
numbers equal to  (or (or  q, depending on what
the "system" is). But the average number of users left behind is simply the
arrival rate q, depending on what
the "system" is). But the average number of users left behind is simply the
arrival rate  times the
average time a random user stays in the "system," times the
average time a random user stays in the "system,"  (or (or  q). q).
3 See also Section 4.9.
|