4.6.5 Extensions and Variations

    Further extensions and variations of the many cases discussed in this section can be developed by permitting the arrival rates and/or the service rates to take the form

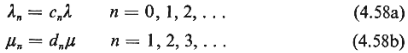
where and are constants and c. and d. are coefficients that depend on the state of the queueing system. (Usually, c_o = 1 and d₁, = 1, so that reflects the rate of demand arrivals when the queueing system is empty and the rate of service when there is only one user in the queueing system.)
    Through (4.58a), one can take into account often-observed phenomena such as reneging and balking. Balking refers to cases in which a prospective user of the queueing system decides, upon arrival at the system and observation of its state, not to wait for its use but (perhaps) to go elsewhere. Reneging is the phenomenon in which users who have already joined the queue become discouraged after a while and leave without obtaining service.
    Similarly, by an appropriate choice of a functional form for d_n, one can account for such phenomena as the often-observed "speed up" of service by human operators whenever queues grow very long. It is easy to imagine how reneging, balking, service speed up or, even, service slowdowns could occur in connection with our emergency center example.
    Commonly used forms of c_n include c_n = (n + j)^-a and d_n. = n^b, where a and b are positive constants. Note how by adjusting a and/or b one can model several types of user behavior. These can be applied with single- or multiserver systems whose capacity is finite or infinite. Although it is usually impossible to obtain closed-form expressions for such quantities as P_n, , , and so on, for these systems, it is often relatively easy to solve numerically the balance equations and tabulate the numerical results (see also Problem 4.2). Such tabulations have been published by several researchers.