4.7 Spatially Distributed Queues And The M/G/1 Queueing
System
As we have already mentioned at the beginning of this chapter,
many queueing systems in
the urban environment do not fit neatly into the classical mold of a
physically stationary
server where prospective "customers" arrive and queue up
until they receive
service. For most of the emergency urban services-where
"arrivals of customers"
are perceived through telephone calls (or other means of
telecommunication) from various
locations in a citythe only place at which a "queue" can
be identified is on the
emergency system's dispatcher's desk (or in a computer's memory),
where records indicate
the time, origin, and nature of a succession of requests for
service. The server, then, be
it a person or a vehicle, must travel to the location of these
incidents to provide the
required service. In such cases we have a spatially
distributed queue.
In this section we shall discuss the simplest
possible type of
spatially distributed queue in which a single server has sole
responsibility for a given
district. This discussion will also motivate our derivation of some
important results for
M/G/1 queueing systems.
Example 1: Ambulance Service to an Emergency
Medical Facility
Consider the case pictured in Figure 4.10: an emergency medical
facility (EMF) is
located at the center (the point where the diagonals intersect) of
a rectangular district
with dimensions X0 ×
Y0 miles.
The EMF has a single ambulance vehicle associated with it, which
is dispatched to
emergency patients and transports them to the EMF. The ambulance,
when idle, is always
located at the EMF.
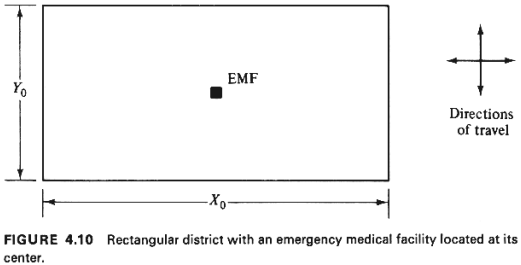
Directions of travel are parallel to the
boundaries of the district
and the effective travel speeds are
vx.
and vy
(constants) in the x and y
directions, as shown in Figure 4.10.
In this district, incidents (each corresponding
to one emergency
patient) occur as a Poisson process in time at a rate of A per
hour. Incident locations
are independent of each other and are uniformly
distributed over the rectangular
area. Every time an incident occurs, the ambulance, if at the EMF,
is immediately
dispatched to the location of the call, picks up the patient, and
returns to the EMF. If
the ambulance is away, calls queue up and are processed in a FIFO
order. We shall assume
for now that no calls are ever lost, no matter how long they have
to wait. We shall also
assume that the pdf for the time, Z, that the ambulance spends at
the location of each
call for service is known and is given by
fz(z) with an expectation Z
and a variance 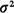 z. z.
The service time, S, in this system clearly
consists of a
"travel-time" component and a "time on the
scene" component. Assuming
that effective travel speeds are identical on both the
EMF-to-incident and the
incident-toEMF portions of each trip, we have

where Tx =
Dx/vx,
and Ty =
Dy/vy,
and Dx and Dy
are defined as the
distances along the x and the y axes, respectively, from (to) the
EMF to (from) the
location of an incident.
With the techniques presented in Chapter 3, it
is an easy matter to
obtain the expected value of S, which for consistency with our
queueing theory notation we
shall denote as 1/ : :
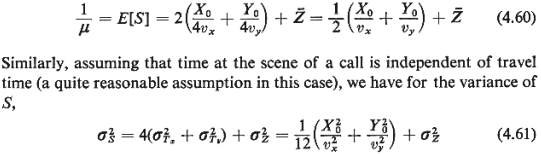
If fz(z),
as we have already
assumed, is known, it is also possible, at least in principle, to
obtain an expression for
fs(s), the service-time pdf. The
derivation, however, even for
the simple situation described here, promises to be tedious and
time-consuming and will be
omitted. It suffices to note that fs(s)
cannot be a negative
exponential pdf [unless
fz(z) is negative
exponential and the expected time on the scene is much
larger than the average
round-trip time, in which case it can be argued that 1/  Z and, therefore, that
fs(s) is
approximately negative exponential as well
7]. It is therefore
clear that results derived for the single-server queueing systems
we have seen so far (M/M/1)
do not apply in this case, since the service-time distribution at
hand is a
"general" one. Z and, therefore, that
fs(s) is
approximately negative exponential as well
7]. It is therefore
clear that results derived for the single-server queueing systems
we have seen so far (M/M/1)
do not apply in this case, since the service-time distribution at
hand is a
"general" one.
We shall now proceed to derive several important results for this
M/G/1 queueing
system. Interestingly, as we shall see, most of the results require
no knowledge of the
service-time distribution, fs(s), other
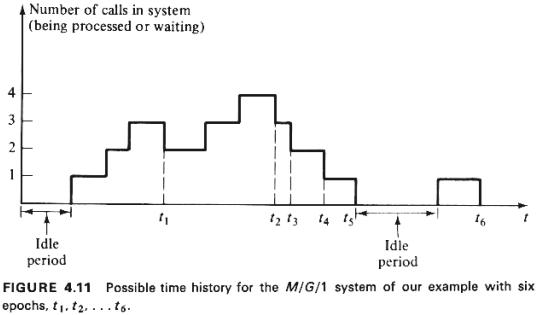
than its mean, 1/ , and variance , and variance 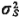 . .
Recall first that the current state of
M/M/1 (or M/M/m)
queueing systems is fully described by a single item of information,
the number of users
(i.e., of calls in our EMF example) currently in the system.
Knowledge of this number is
sufficient to describe all the past history of the queueing system,
as far as the future
is concerned. For instance, if it is known that at some time
instant, t, there are exactly
n (> 0) calls in a M/M/1 system (with one call receiving
service and the other n -
1 calls in the waiting line), then we can immediately state that the
probability thatin
the next 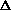 t a service will be completed is
equal to t a service will be completed is
equal to  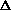 t-independently
of what else has happened in the past at that M/M/1 system. For
M/G/1 systems, however,
this probability also depends on how long ago service began to the
call that is currently
receiving service. Thus, a complete description of the current state
of a M/G/1 system
requires, in general, specification of the values of two random
variables, the number of
calls currently in the system, and the time since the current
service began, the latter of
which is a continuous random variable. These complications make the
mathematical analysis
of M/G/1 systems more difficult than that of M/M/1 or
M/M/m systems. t-independently
of what else has happened in the past at that M/M/1 system. For
M/G/1 systems, however,
this probability also depends on how long ago service began to the
call that is currently
receiving service. Thus, a complete description of the current state
of a M/G/1 system
requires, in general, specification of the values of two random
variables, the number of
calls currently in the system, and the time since the current
service began, the latter of
which is a continuous random variable. These complications make the
mathematical analysis
of M/G/1 systems more difficult than that of M/M/1 or
M/M/m systems.
Of the several different approaches that have
been developed, the
simplest one uses the trick of focusing attention on certain
specific instants in time,
known as epochs, when knowledge of only the number of calls
currently in the
queueing system is sufficient to specify its current state. Those
instants of time are the
times of completion of a service by the server (i.e., the instants
after the ambulance has
returned to the EMF and delivered a patient, in the case of our
example).
Let us then indicate these time instants as
t1,
t2,
t3 .
. . with ti, representing the instant when service to the
ith patient to be
transported to the EMF (beginning with some arbitrary time t = 0) is
completed. A specific
example for a hypothetical M/G/1 queueing system is shown in Figure
4.11.
We can then define:
N = number of calls in the queueing system (i.e., the number of
patients/incidents
waiting for service) just after the instant
ti-1
when service to the (i - 1)th patient is completed
R = number of new calls that arrive at the queueing
system during the service
time of the next patient to receive service (patient i)
N' = number of calls in the queueing system just after
ti,
the instant of completion of service to patient i
Note that, by definition, R includes only
those calls that arrive at
the queueing system after service to the next patient
(patient i) has
started. This is important for the cases when, upon completion of a
service, the queueing
system is left empty (i.e., no more calls left to serve). For
instance, the value of R for
the time interval between
t5 and
t6,
is 0 (not 1) for the sample case shown in Figure 4.11.
The following relationship exists between the
random variables N, R,
and N':
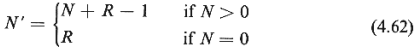
The probability 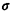 r, that exactly r calls
arrive during a service
time is given by r, that exactly r calls
arrive during a service
time is given by
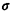 r = P{number of new
arrivals during a service time= r}
=
pR(r) r = P{number of new
arrivals during a service time= r}
=
pR(r)
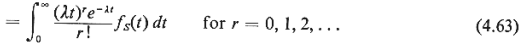
where, as above, fs(s) represents the pdf for
the service time. For
any given pdf f,(s), it is then possible to determine the
probabilities 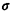 r. r.
Exercise 4.5 How is (4.63) justified?
Hint: Given that a service lasted exactly a time t, what is
the probability that
r new calls arrived during that service time?
For r = 0, 1, 2,. . . , we have

So (4.64) and (4.65) give the state-transition probabilities for
successive epochs for
the M/G/1 system. The state-transition diagram for our M/G/1 system,
at the epochs is now
shown in Figure 4.12. A state is defined by

"the number of calls present at the time when a service is
completed." Note
that the state-transition diagram of Figure 4.12 is no longer of the
birth-and-death type.
In the analysis that follows, we shall be
interested only in the
expected values  , ,  , ,  , and , and  q, which can be
derived without using
the state-transition diagram. We shall, therefore, ignore Figure
4.12 from here on. q, which can be
derived without using
the state-transition diagram. We shall, therefore, ignore Figure
4.12 from here on.
Let us define a random variable 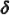 such that such that

Note that (4.72) has a very real meaning: from the definition
of 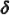 ,
it follows that E[ ,
it follows that E[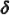 ]
is equal to the
fraction of epochs, ti at which the queueing system will be
found empty upon
completion of a service. It follows that (4.72) cannot be meaningful
unless 8 ]
is equal to the
fraction of epochs, ti at which the queueing system will be
found empty upon
completion of a service. It follows that (4.72) cannot be meaningful
unless 8
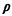 < 1 ( < 1 ( < <  ). This is also the
condition under which steady state exists for M/G/1 systems. ). This is also the
condition under which steady state exists for M/G/1 systems.
Let us now square both sides of (4.67) to obtain
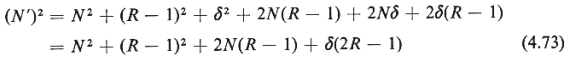
where we have used the facts that 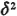 = = 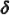 and that 2N and that 2N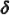 = 0 (both resulting directly from the
definition of = 0 (both resulting directly from the
definition of 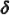 ).
Taking now the
expected values of both sides of (4.73) and noting that in the
steady state
E[(N')^2]1 = E[N^2], we have ).
Taking now the
expected values of both sides of (4.73) and noting that in the
steady state
E[(N')^2]1 = E[N^2], we have
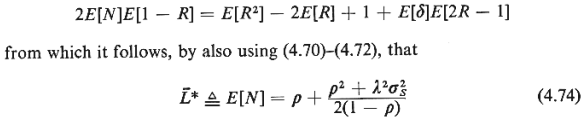
We have used the asterisk in (4.74) to indicate that  * denotes the
expected number of users
in the system at the instants that follow the service
completions on which we
have concentrated, the epochs. * denotes the
expected number of users
in the system at the instants that follow the service
completions on which we
have concentrated, the epochs.
It turns out that  * is equal to * is equal to  , the expected number of calls in the
queueing system that
would be observed by someone arriving at a random time with the
system in the steady
state. To show this, it suffices to show that the steady-state pmf
for the number in the
system at the instants of service completion is identical to the
steady-state pmf for the
number in the system at any random instant. This we now proceed to
do in a rather informal
way. We define , the expected number of calls in the
queueing system that
would be observed by someone arriving at a random time with the
system in the steady
state. To show this, it suffices to show that the steady-state pmf
for the number in the
system at the instants of service completion is identical to the
steady-state pmf for the
number in the system at any random instant. This we now proceed to
do in a rather informal
way. We define
 n
= steady-state probability that just after the completion of a
service there are n calls
left in the queueing system n
= steady-state probability that just after the completion of a
service there are n calls
left in the queueing system
Pn = steady-state
probability that a
call arriving at the system at a random time will find n
calls in the queueing
system
Jn = number of "downward
jumps" from n + 1
to n (in the number of calls in the queueing system)
which are observed
during a time interval T
J = 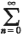 Jn = total number of downward jumps in the
number of calls in
the queueing system observed during the time interval T
Jn = total number of downward jumps in the
number of calls in
the queueing system observed during the time interval T
Kn = number of
"upward jumps" from n
to n + 1 (in the number of calls in the queueing system) which are
observed during the
time interval T
K = 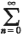 Kn
= total number of upward jumps in the number
of calls in the
queueing system observed during the time interval T Kn
= total number of upward jumps in the number
of calls in the
queueing system observed during the time interval T
Obviously, downward jumps are due to service
completions and upward
jumps are due to call arrivals. Obviously, too, the quantities
Jn
and Kn can differ by at
most 1 unit during any
time interval T.
Assuming that the queueing system does reach
steady state, we have,
from the definition of  n, that n, that

Also, since steady state is reached, the number of upward jumps
must be about the same
as the number of downward jumps (i.e., the ratio of J to K must go
to 1 as T goes to
infinity). From this, plus the fact that
Jn and
Kn
differ at most by one and from (4.75), we then have

The right-hand side above is the steady-state
probability that the
system is in state n at the instant of an arrival.
Arrivals, however, occur in a
Poisson manner, meaning that the instants of arrivals are
completely random! Thus,
lim t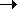 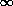 (Kn/K)
= Pn and we have shown that
(Kn/K)
= Pn and we have shown that

for the M/G/1 queueing system. These results are valid for
steady-state conditions
which exist whenever
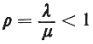
Expressions (4.78)-(4.82) are remarkable for
their simplicity, since
they apply to any service-time distribution. [In fact, in deriving
these expressions we
made no assumptions whatsoever about the specific form of
fs(s).]
They are usually referred to as the "Pollaczek-Khintchine
formulas." To use
them, all that is needed to know about the service time is its
expected value and its
variance-which is certainly most convenient in practical
applications. It is also
important to note that  (as well as (as well as  , ,  q, and q, and  q) depends on
the variance of the service times: increasing the consistency of
service (i.e., reducing
the variance of service times) improves the performance of the
service facility. q) depends on
the variance of the service times: increasing the consistency of
service (i.e., reducing
the variance of service times) improves the performance of the
service facility.
Several additional results have been obtained
with regard to the
M/G/1 queueing system. For instance, from (4.78) we can conclude
that the following ratio
holds:
E[length of busy period] =
fraction of time system is
busy = 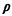 /(1- /(1-
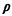 ) )
E[length of idle period] = fraction of time system is
idle
But since E[Iength of idle period] = 1/ (since we have Poisson
arrivals with rate (since we have Poisson
arrivals with rate  ), it can be
concluded that ), it can be
concluded that
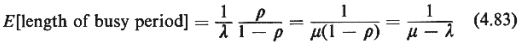
Interestingly, (4.83) is identical with (4.43), the expression
for the expected length
of the busy period for M/M/1 queueing systems.
For a given service time pdf,
fs(s),
it is also possible to obtain expressions (or numerical estimates)
for the steady-state
probabilities, Pn. This is accomplished by
first obtaining an
expression for the geometric transform of these probabilities (see,
for instance, [GROS
74]).
Example 1 (continued)
To illustrate some of the above, let us take
XO
= 2 miles, YO = 1 mile,
vx,
30 miles/hr, vy, = 20 miles/hr, 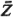 = 10 minutes,
and = 10 minutes,
and 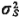 = 25 minutes2. = 25 minutes2.
Solution
It follows from (4.60) and (4.61) that l/ = 13.5 minutes and = 13.5 minutes and 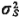 = 27.1
minutes = 27.1
minutes . Thus, the
service rate . Thus, the
service rate  =
4.44 calls/hr. We can then derive the following table, for
different demand (call) rates, =
4.44 calls/hr. We can then derive the following table, for
different demand (call) rates,  , under
steady-state conditions: , under
steady-state conditions:
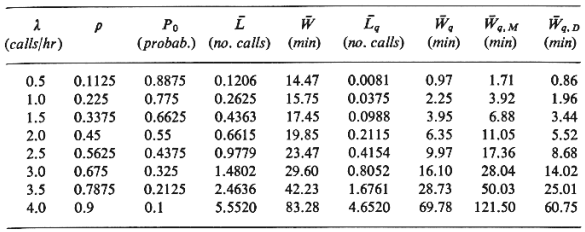
The quantities
PO,
 , ,  , , q , and q , and
 q
in this table have been computed by using relations (4.78)-(4.82). q
in this table have been computed by using relations (4.78)-(4.82).
 q,M
and q,M
and  q.D,
the quantities listed in the two rightmost columns represent
the average waiting
time for the corresponding M/M/1 and M/D/1 systems, respectively.
That is, q.D,
the quantities listed in the two rightmost columns represent
the average waiting
time for the corresponding M/M/1 and M/D/1 systems, respectively.
That is,  q,M
has been computed for a single-server system with negative
exponential service time
distribution and an expected service time, 1/ q,M
has been computed for a single-server system with negative
exponential service time
distribution and an expected service time, 1/ , of 13.5 minutes; similarly, , of 13.5 minutes; similarly,
 q,D corresponds
to a constant service time equal W 13.5 minutes. Since an M/M/1
system can be viewed as
just a special case of M/G/1, it is hardly surprising that when we
set q,D corresponds
to a constant service time equal W 13.5 minutes. Since an M/M/1
system can be viewed as
just a special case of M/G/1, it is hardly surprising that when we
set 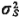 = 1/ = 1/  (negative
exponential service times) in (4.79)-(4.82), the expresssions for
the corresponding M/M/1
quantities are obtained. (Try one!) Similarly, the expressions for
the M/D/1 system can be
obtained by setting (negative
exponential service times) in (4.79)-(4.82), the expresssions for
the corresponding M/M/1
quantities are obtained. (Try one!) Similarly, the expressions for
the M/D/1 system can be
obtained by setting 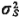 = 0 in (4.79)-(4.82). A particularly
simple and useful
relationship to remember is that = 0 in (4.79)-(4.82). A particularly
simple and useful
relationship to remember is that

As one might expect from the fact that 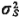 < 1/ < 1/  in our example, the
values of in our example, the
values of  q, for
all values of q, for
all values of  in the table fall between the
corresponding values of in the table fall between the
corresponding values of  q,m and q,m and
 q,d.
In fact, there is a particularly convenient form for expressions
(4.79)-(4.82) that brings
out clearly the significance of the term that includes the
variance of the service time:
we can use the coefficient of variation Cs,( q,d.
In fact, there is a particularly convenient form for expressions
(4.79)-(4.82) that brings
out clearly the significance of the term that includes the
variance of the service time:
we can use the coefficient of variation Cs,( 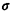 s /
E[S] = s /
E[S] = 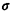 s. s.
 ) for the service
time to rewrite, say, (4.79) as ) for the service
time to rewrite, say, (4.79) as
(Remember that for negative exponential service times
Cs = 1 and
for constant service times Cs = 0.)
Finally, to conclude the exanple, we might want
to review the table of
numerical results to assess the Performance of the ambulance
service that we have
described. It is interesting, for instance, that at an arrival
rate of 1.5 calls/hr, the
average delay before the ambulance is dispatched to a random call
for service is about 4
minute-longer than what it takes for the ambulance, on the
average, to travel from the
EMF to the point from which the call has originated and back (=
3.5 minutes). And this,
despite the fact that, for  = 1.5, the ambulance is busy
(traveling or at the scene of an
incident) only about one third of the time. It is thus very likely
that emergency medical
service administrators would find the level of service (as
manifested by the average
dispatch delay, = 1.5, the ambulance is busy
(traveling or at the scene of an
incident) only about one third of the time. It is thus very likely
that emergency medical
service administrators would find the level of service (as
manifested by the average
dispatch delay,  q) provided by this single
ambulance emergency
medical system to be unacceptable for call rates greater
than 1.5 or, at most, 2.0
calls/hr. q) provided by this single
ambulance emergency
medical system to be unacceptable for call rates greater
than 1.5 or, at most, 2.0
calls/hr.
What to do, then? We might attempt to speed up
service (reduce 1/ ) or
"standardize" the service (reduce ) or
"standardize" the service (reduce 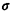 2s). Suppose that a 20
percent decrease could be
achieved for 1/
2s). Suppose that a 20
percent decrease could be
achieved for 1/ [i.e., we could achieve 1/
[i.e., we could achieve 1/ ' = (13.5)(0.8) = 10.8 minutes]. Then
for, say, ' = (13.5)(0.8) = 10.8 minutes]. Then
for, say, = 3.0, we
would obtain = 3.0, we
would obtain  q'
= 7.82 (assuming that q'
= 7.82 (assuming that 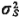 stays constant at 27. 1). This is a
better than 50 percent
reduction in average S dispatch delay! stays constant at 27. 1). This is a
better than 50 percent
reduction in average S dispatch delay!
Suppose, instead, that we could reduce the
standard deviation of
service times by 20 percent [i.e., that we could achieve 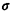 ''s =
(0.8)(27.1)1/2
or, in other words ( ''s =
(0.8)(27.1)1/2
or, in other words (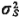 )" = (0.64)(27.1) = 17.341.
Then for )" = (0.64)(27.1) = 17.341.
Then for  = 3.0, and
assuming that 11p remains constant at 13.5, we would obtain = 3.0, and
assuming that 11p remains constant at 13.5, we would obtain  q'' =
15.35 minutes or an
improvement of only about 5 percent over the original q'' =
15.35 minutes or an
improvement of only about 5 percent over the original  q of
16.1 minutes. In
general, reductions in expected service times are usually much
more effective than
comparable reductions in the variance of service times. This
should be obvious from the
fact that changes in the expected service time, 1/ q of
16.1 minutes. In
general, reductions in expected service times are usually much
more effective than
comparable reductions in the variance of service times. This
should be obvious from the
fact that changes in the expected service time, 1/ affect both the numerator
and denominator of
(4.79)-(4.82) by changing the utilization factor, p. affect both the numerator
and denominator of
(4.79)-(4.82) by changing the utilization factor, p.
When it is not possible to reduce 1/ or or 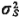 to achieve improved perfor S mance for
a given demand rate to achieve improved perfor S mance for
a given demand rate  , one has to
resort to more drastic measures, such as increasing the number of
ambulances in our
present example or reducing the area of responsibility of the EMF
(and thus , one has to
resort to more drastic measures, such as increasing the number of
ambulances in our
present example or reducing the area of responsibility of the EMF
(and thus  as well).
With m ambulances at hand (m > 1) that would mean an M/G/m
queueing system, which we
proceed to discuss next. A more "complicated" spatially
distributed M/G/1
queueing system will be discussed in Section 5.2. as well).
With m ambulances at hand (m > 1) that would mean an M/G/m
queueing system, which we
proceed to discuss next. A more "complicated" spatially
distributed M/G/1
queueing system will be discussed in Section 5.2.
7 It turns out that this is often the case with some
important urban emergency
services, such as police and most emergency repair services.
This makes possible the
derivation of many powerful results with respect to these
services (see Chapter
5).
8 It can be shown that steady state is not reached when
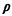 = 1. Expected
queue lengths and expected waiting times are infinite for
that value of = 1. Expected
queue lengths and expected waiting times are infinite for
that value of 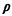 . .
|