4.10 "Output" of a M/M/1 system In this
problem you are asked to
prove the important theorem of Section 4.10 for the case of a M/M/1
queueing system. Let a
queueing system with a single server have Poisson arrivals at a rate
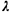 , infinite
queue capacity, and negative exponential service time with mean
1/ , infinite
queue capacity, and negative exponential service time with mean
1/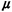 ( (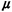 > > 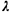 ). Show that in the steady
state the
"output" stream leaving this queueing system is also
Poisson at a rate ). Show that in the steady
state the
"output" stream leaving this queueing system is also
Poisson at a rate 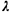 . .
Hint: What is the pdf for the time between service
completions when the
server is continually busy?
|