4.11 "User-optimal" versus "system-optimal"
equilibrium Two
different facilities, A and B, provide the same type of service.
Each facility contains a
single server with service times distributed as negative exponential
random variables. The
mean service times are 1/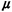 1=1 minute and 1/ 1=1 minute and 1/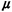 2
= 4 minutes at facilities A and B, respectively. Other than the
different expected length
of service times, the service that A and B provide is identical (in
terms of quality, cost
to the user, etc.). (Think, for instance, of two truck-weighing and
inspection facilities
that differ only by the rate at which they inspect trucks.) 2
= 4 minutes at facilities A and B, respectively. Other than the
different expected length
of service times, the service that A and B provide is identical (in
terms of quality, cost
to the user, etc.). (Think, for instance, of two truck-weighing and
inspection facilities
that differ only by the rate at which they inspect trucks.)
A combined total of 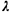 = 60
customers per hour wish to avail themselves of the service provided
by facilities A and B.
The situation is pictured in Figure P4.11. Arrivals of customers at
the critical point are
Poisson. At that point each customer makes a choice, independently
of all others, on which
facility he or she is going to use. This choice is made without any
knowledge of the
status of the queue in front of either facility. Let p denote the
probability that a
random customer chooses facility A (and 1 - p that he or she chooses
B). = 60
customers per hour wish to avail themselves of the service provided
by facilities A and B.
The situation is pictured in Figure P4.11. Arrivals of customers at
the critical point are
Poisson. At that point each customer makes a choice, independently
of all others, on which
facility he or she is going to use. This choice is made without any
knowledge of the
status of the queue in front of either facility. Let p denote the
probability that a
random customer chooses facility A (and 1 - p that he or she chooses
B).
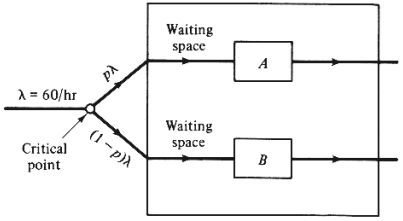
a. Consider the case when the same pool of customers use
facilities A and B on a
repeated basis (say, once every day). (Think, for instance, of
suburban commuters in a
town with two major access roads to the central business district.
Each of these commuters
decides every day, independently of all others, which of the two
roads he or she is going
to use that day, without knowledge of traffic conditions on either
road.) Let us assume
that each user is only concerned with minimizing his or her
expected time spent in a
service facility, 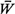 (= average waiting time + average
service time). It can be
reasonably expected that in the long run (system in steady state
and in equilibrium-as far
as the distribution of customers between the two facilities is
concerned) the customers
will "distribute" themselves among the two facilities,
in the sense that p
will stabilize around a specific value. What is that value of
p? (= average waiting time + average
service time). It can be
reasonably expected that in the long run (system in steady state
and in equilibrium-as far
as the distribution of customers between the two facilities is
concerned) the customers
will "distribute" themselves among the two facilities,
in the sense that p
will stabilize around a specific value. What is that value of
p?
b. Suppose now that your objective is to minimize the total
amount of time (waiting and
being serviced) that all customers spend in either of the two
facilities per unit of time
(with the system in the steady state). This is equivalent to
minimizing, say, the
"cost" suffered by the community each day, where cost is
measured in terms of
total commuter hours spent in traffic. You can thus set the value
of p yourself (and thus
force each arriving customer, independently, to choose between the
two facilities on the
basis of your p). What would you choose as the value of
p?
Note: Feel free to use trial and error (rather than
an "elegant"
approach) in determining p.
c. Can you explain intuitively why the answers to parts (a) and
(b) are different? Can
you suggest a situation parallel to the one above in highway
traffic and how it might be
possible to achieve the value of p that you found in part (b) in
this case?
|