4.6 Spatially distributed queue with random server location In this problem we
examine a spatially distributed queueing system similar to that of Example 1, Section 4.7.
In the process we shall examine how the "advantage of central location" (i.e.,
the benefits of positioning a facility/server at the geographical center of an urban area)
behaves as a function of system utilization. In this problem the server will be randomly
located in the district, in contrast to Example 1, in which it was centrally located.
We shall examine here the case in which the rectangular
district of Figure 4.10 is patrolled by a police car which is dispatched to incidents
within the district. Incidents are served in a FCFS manner, with the patrol car traveling
from incident to incident whenever there is a backlog of calls for police assistance. At
times when no pending calls exist and the patrol car is free, it remains stationary at
the location of the last incident that it served, waiting to be dispatched to the
next call for assistance. All other assumptions in the problem (e.g., right-angle travel,
uniformly distributed incidents in the district, Poisson demands, service time on the
scene, travel speeds, etc.) are identical to those of Example 1. It will be assumed,
however, that the dimensions of the district are now 2X0
× 2Y0 miles. This is done to make the results of
this problem comparable to those of Example 1, where the ambulance must make round
trips between the hospital and the incidents that it serves.
a. Obtain expressions for 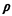 , ,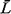 , , 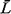 q, q, 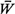 , and , and 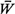 q, in this case. To avoid any confusion, we specify
that the patrol car "begins serving" a particular incident, as soon as the
patrol car begins its trip toward that incident. You should also assume that successive
service times (= travel time + time on the scene) are statistically independent. [In
truth, there is a slight correlation between successive service times (why?).] q, in this case. To avoid any confusion, we specify
that the patrol car "begins serving" a particular incident, as soon as the
patrol car begins its trip toward that incident. You should also assume that successive
service times (= travel time + time on the scene) are statistically independent. [In
truth, there is a slight correlation between successive service times (why?).]
b. Assuming exactly the same numerical values as in Example 1 (numerical example),
prepare a table for 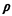 , ,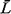 , , 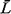 q, q, 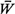 , and , and 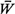 q, as the rate of calls per hour, A, increases.
Compare these values to those for the ambulance service of Example 1. How do these values
differ as q, as the rate of calls per hour, A, increases.
Compare these values to those for the ambulance service of Example 1. How do these values
differ as 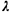 increases (
increases (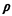 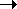 1) ? 1) ?
|