4.7 Planning for a large parking garage A parking garage is planned for a
large airport which is wholly owned by a city. This garage will serve the needs of
"park-and-fly" passengers at one major section of the airport. it has been
decided that the garage's capacity will be geared to the peak season of the airport, which
consists of about five consecutive months. The planners believe that the demand (i.e., the
number of cars seeking a parking spot at that section of the airport) can be reasonably
modeled as a Poisson process with a mean, 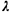 , of about 2,500 cars per day. The time during
which any given parking spot is occupied by a car is assumed to be a random variable with
some arbitrary pdf, a mean (1/ , of about 2,500 cars per day. The time during
which any given parking spot is occupied by a car is assumed to be a random variable with
some arbitrary pdf, a mean (1/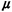 ) = 30 hours, and finite variance. It has been decided, after
much debate, to provide sufficient capacity at the garage so that "a motorist will be
able to find a free space there 98 percent of the time"-with a new system planned to
direct motorists to areas with free parking spaces. Assuming that drivers who are
informed, at the time when they seek entry, that the garage is full will become
discouraged and go somewhere else: ) = 30 hours, and finite variance. It has been decided, after
much debate, to provide sufficient capacity at the garage so that "a motorist will be
able to find a free space there 98 percent of the time"-with a new system planned to
direct motorists to areas with free parking spaces. Assuming that drivers who are
informed, at the time when they seek entry, that the garage is full will become
discouraged and go somewhere else:
a. Estimate approximately how many parking spaces should be provided at the garage.
Justify your reasoning, possibly with reference to some queueing theory model.
b. Based on your analysis for part (a)-and provided that all other assumptions in the
model are reasonable-discuss which is more important in planning for the size of the
garage: the accuracy of the estimated values of 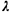 and 1/ and 1/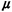 , or the probability of parking availability sought
(e.g., 98 percent)? , or the probability of parking availability sought
(e.g., 98 percent)?
|