5.3.1 Restrictions on Service Time
and Queueing Behavior
As we will see, as we proceed from 1 to 2 to N servers, the
restrictions we must place on the service-time distribution become more
and more severe. With this N = 2 model, we assume that the two
servers have the same (general) service-time distribution with mean 1 /
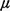 . Successive service times must represent
independent samples from this distribution, independent of the history
of the system, its current state, the identity of the responding unit,
or the location of the service request. Thus, unlike the M / G /
1 model (or its modification in the previous section), the N
= 2 model cannot explicitly include variations in service times due
solely to variation, say, in customer location or server identity. This
does not mean that travel time must be ignored in the service time. To
the contrary, the mean service time can be set equal to the sum of the
estimated mean travel time (estimated prior to the analysis), the
on-scene time, and any related off-scene follow-up time. After analysis,
mean travel time is a model-computed performance measure; if there is a
discrepancy between the estimated and the computed mean travel times,
the computed mean travel time should be used to revise the model's mean
service time parameter and the analysis should be performed again with
the revised value. This iterative procedure, called mean service-time
calibration, usually converges very quickly (typically one or two
iterations). After calibration, the mean travel time assumed in
computing mean service time agrees with that computed by the model.
Throughout the following model development, we will assume that such
calibration has occurred. . Successive service times must represent
independent samples from this distribution, independent of the history
of the system, its current state, the identity of the responding unit,
or the location of the service request. Thus, unlike the M / G /
1 model (or its modification in the previous section), the N
= 2 model cannot explicitly include variations in service times due
solely to variation, say, in customer location or server identity. This
does not mean that travel time must be ignored in the service time. To
the contrary, the mean service time can be set equal to the sum of the
estimated mean travel time (estimated prior to the analysis), the
on-scene time, and any related off-scene follow-up time. After analysis,
mean travel time is a model-computed performance measure; if there is a
discrepancy between the estimated and the computed mean travel times,
the computed mean travel time should be used to revise the model's mean
service time parameter and the analysis should be performed again with
the revised value. This iterative procedure, called mean service-time
calibration, usually converges very quickly (typically one or two
iterations). After calibration, the mean travel time assumed in
computing mean service time agrees with that computed by the model.
Throughout the following model development, we will assume that such
calibration has occurred.
One additional price we pay for a general service-time distribution
(rather than, say, an exponential distribution) is that no queue is
allowed to form. That is, customers that appear when both units are
busy are not serviced by the N = 2 system. We suppose that, in
reality, they are handled by some backup system (such as a police
department backing up an ambulance service). If we had desired a queue
of arbitrary length to be allowed, we would have to restrict further our
service-time assumption, requiring the distribution to be negative
exponential. This is another example of how an apparently simple
modification of a queue's operating behavior can change markedly the
ease or difficulty of analyzing the queue.
|


