


5.3.2 General ModelWe consider a region B served by two response units, unit 1 and unit 2. Each unit, while not busy at a service request, is located at a fixed home location or facility. The system operates in the following way: If X is any subset of B, we assume that
service requests arrive in X according to a Poisson process with
parameter The region is partitioned into two primary response areas,
area 1 comprising the set A and area 2 comprising the set B -
A. Requests for service arrive from area 1 with rate If an area n service request arrives when both units are available, it is served by unit n, n = 1, 2. If an area n service request arrives when exactly one unit is available, it is served by the available unit, n = 1, 2. If an area n service request arrives when neither unit is available, the request is lost. As discussed above, this assumption usually implies that the request is handled by some backup service system. The system is operating in the steady state. The service times for all service requests are identically
distributed with a finite average 1 / Each server can be in one of two states: 0, corresponding to available or free; and 1, corresponding to busy servicing a request. There are thus 22 system states, as follows:
(Note that the status of unit n is given by the nth digit from the right in the binary-state depiction.) As we will see in the next section, the binary-state classification extends in a natural way to N servers, in which case the system has 2N states.
The state-transition diagram for this four-state process is shown in Figure 5. 1. While the steady-state probabilities do not depend on the exact form of the service time distribution [CHAI 731, we will assume negative exponential service times, in order to write the equilibrium equations of balance in accordance with the procedures of Chapter 4:
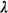 = (P01 +
P10) = (P01 +
P10)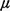
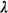 + + 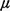 ) = P00 ) = P00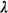 1 + P11 1 + P11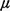
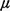 = P01 = P01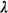 + P10 + P10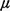
Substituting (5.8) into (5.6) yields
Substituting (5.10) into (5.7) yields
By symmetry we must have
Finally, substitution into (5.9) yields (after some manipulation)
We notice that P00 is the same as P{S0} in an
M / M / 2 system with no waiting space. This is just what we
expect: the two-server system that we are analyzing is simply an M /
M / 2 system with distinguishable servers with no waiting space.
Defining
We define the workload of unit n to be the steady-state
probability that unit n is servicing a request, and we denote it
by
The difference in workload
Another quantity of interest is This "interarea dispatch frequency" allows us to compute mean travel times. Define
Then, for instance, Tn(B) is the average travel time if every serviced request (in B) is answered from location n. Since region A is unit 1's primary response area, the average system-wide travel time to serviced requests can be written
How do we obtain the fnj's? Invoking an argument of
Chapter 2, consider a long time interval T. In the steady state,
the average total number of requests serviced is (1 -
P11)
In a similar manner, we find that
Substituting (5.15) and (5.16) into (5.14), we obtain for the mean travel time,
This formula can be used to calculate mean travel time for any proposed primary response areas A and B - A. |