


5.3.3 Nonhomogeneous Rectangular City Example
We consider as an example the rectangular city shown in Figure 5.2. This city runs 2 miles east-west and 1 mile north-south with an x-y coordinate system centered at the city center. Travel time is assumed to be proportional to travel distance; the travel distance between any two points (xi, yi) and (xj, yj) is given by the Manhattan metric,
The home location for unit 1 is x1 = +0.75,
y1 = 0.0 and for unit 2 is x2 =
-0.25, y2 = 0.0. Requests for service are
unevenly distributed, with fully 50 percent of the requests
distributed uniformly over the region east of facility 1 (x >
0.75). The remaining half of the requests for service are distributed
uniformly over the rest of the city (x It is decided that the primary response areas for the two units will
be determined by a boundary line located a distance w west of facility 1
(and 1 - w east of facility 2). We assume that 0
Using the general formulas given above, we arrive at expressions as
functions of w for Equal-travel-time boundary line. A most sensible partitioning of the city into the two primary response areas would entail setting w = 1/2, equidistant from facilities 1 and 2, yielding response areas Aw = 1/2 and B - Aw = 1/2. With such a partitioning, requests are always assigned to the closest available unit, thereby minimizing the "immediate cost of response," where cost is measured by mean travel time. One might think that such a policy would minimize overall system mean travel time. Substituting all the numerical values describing this problem into (5.17), we obtain the system mean travel time,
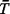 (Aw =
1/2) = 0.46246 (Aw =
1/2) = 0.46246
 1 = 0.49010 1 = 0.49010 2 = 0.43773 2 = 0.43773
yielding a workload imbalance
 1 - 1 -  2| = 0.05236 2| = 0.05236
Alternative boundary line. If we believe that w =
1/2 yields minimum system-wide mean travel time, we should be able to
verify that by differentiation of The differentiation is straightforward since w appears in T only additively in the forms k1w and k2w2. Substituting the equations in Table 5-3 into (5.17), we obtain 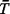 /dw = 0 = w -
53/126 /dw = 0 = w -
53/126
implying that the optimal value for w, denoted w*, is Response area 1, now denoted Aw*, has
its western boundary shifted to the right of the equal-travel-time
boundary line by 10/126 = 0.0794 mile. In the "shifted" region,
corresponding to 1/2 The interested student may well wonder what savings in mean travel time are obtained in this example by following an optimal boundary-line policy. The result is
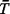 (Aw*) =
0.46166 (Aw*) =
0.46166
or only 0.173 percent less than the equal-travel-time boundary line. This result is consistent with other analysis of spatially distributed probabilistic systems, which show that mean travel time is rather insensitive to slight changes in system boundaries. What is surprising about the boundary line that minimizes mean travel time is its effect on workload imbalance. With w = w* = 53/126.
 1 = 0.44189 1 = 0.44189 2 = 0.48594 2 = 0.48594
yielding a workload imbalance of 0.04405, compared to the earlier value of 0.05236, or a 15.87 percent improvement in this measure. Thus, by designing the system to minimize one performance measure, we obtain an improvement in another performance measure. This is unusual in operations research, where one usually must confront trade-offs requiring degradation in one measure of performance to achieve improvement in another. In applications, Carter, Chaiken, and Ignall, who originally analyzed the two-server model, and later Jarvis, who extended the ideas to N servers, have used the developed procedures for minimizing mean travel time primarily to achieve reductions in workload imbalance. So, here we have a rather strange situation in which algorithms and procedures developed for optimizing one system of performance measure are used in practice to achieve improvements in another performance measure. |