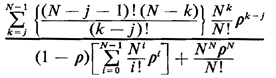5.5.1 Correction Factor
In an M / M / N queueing system with infinite queueing
capacity, suppose that we start randomly sampling servers in the
system until we find the first server who is available or free (if there
is one). Let
Bj 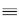 event that jth
selected server is busy (not available) event that jth
selected server is busy (not available)
Fj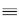 BjC = event that jth server selected
is free (or available)
BjC = event that jth server selected
is free (or available)
P{B1B2. . .
BjFj+1} 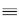 probability that the first free server is the
(j + 1)st server selected probability that the first free server is the
(j + 1)st server selected
The server selection process here is a strictly random sampling
without replacement. In effect, we are selecting servers in a
"blindfolded" manner.
Now the probability
P{B1B2. . .
BjFj+1} corresponds, in an
urban services context, to a dispatch probability, that is, the
probability of assigning the (j + 1)st preferred server to a
service request. If the nth server selected, say server
sn, is busy a fraction of time  sn, then a naive
approach would be to assume that servers operate independently. In that
case, we would have sn, then a naive
approach would be to assume that servers operate independently. In that
case, we would have
P{B1B2. . .
BjFj+1} 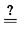  s1 s1 s2. . . s2. . .  sj(1 - sj(1 -  sj+1 sj+1 |
j < N |
P {B1B2. . .
BN} 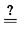 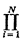  si si
We can see by inspection that this is mathematically incorrect since
{B1B2. . . BN}
corresponds to the probability of saturation of the M / M / N
system (i.e., all servers are simultaneously busy) and, as shown by
(4.44), this is not equal to the product of utilization factors.
We can still utilize the multiplicative concept if we incorporate a
suitable "correction factor." To do this, we write
|
P{B1B2. . .
BjFj+1} =
P{Fj+1 |
B1B2. . .
Bj}P{Bj |
B1B2. . . Bj-1}. .
. P{B1}
|
(5.45)
|
Multiplying both numerator and denominator of the right-hand side by
 j(1 - j(1 -  ), we have ), we have
P{B1B2. . .
BjFj+1}
= 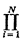  j(1 - j(1 -  ) )
(5.46)
If we define Q(N, p, j) to be the term preceding pJ(1 - p), we
have
| P{B1B2.
. . BjFj+1} | (5.47) |
The factor Q(N,  , j) indicates the
extent to which the result of the server-independence argument must be
"corrected" to obtain the exact result. Each of the j + 1 terms
in the product comprising Q(N, , j) indicates the
extent to which the result of the server-independence argument must be
"corrected" to obtain the exact result. Each of the j + 1 terms
in the product comprising Q(N,  , j) can
be considered to be a separate correction factor indicating the relative
amount by which , j) can
be considered to be a separate correction factor indicating the relative
amount by which  or 1 - or 1 -  overestimates (or underestimates) the respective conditional
probabilities of being busy or free. As shown in Problem 5.9, the exact
expression for Q(N,
overestimates (or underestimates) the respective conditional
probabilities of being busy or free. As shown in Problem 5.9, the exact
expression for Q(N,  , j) can be derived
by conditioning on each possible number of servers busy in an M / M /
N system, and then combining results by laws of conditional
probability. The result is , j) can be derived
by conditioning on each possible number of servers busy in an M / M /
N system, and then combining results by laws of conditional
probability. The result is
Q(N,  , j) = , j) = 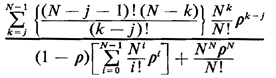
| j = 0, 1, . . . , N - 1 |
| (5.48) |
In checking the result for a limiting case, we find that Q(N,  , 0) = 1, indicating that the probability that the
first selected server is free is exactly 1 - , 0) = 1, indicating that the probability that the
first selected server is free is exactly 1 -  (a
result in agreement with intuition, since (a
result in agreement with intuition, since  = =
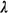 /N /N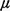 is the
average fraction of time a server is busy). Additional work shows that
Q(N, is the
average fraction of time a server is busy). Additional work shows that
Q(N,  , 1) < 1, which implies that , 1) < 1, which implies that  (l - (l -  ) is an overestimate of
P{B1F2}. This is true since,
given that the first selected server is busy, the probability
P{F2 | B1} that the second
selected server is free is less than (1 - ) is an overestimate of
P{B1F2}. This is true since,
given that the first selected server is busy, the probability
P{F2 | B1} that the second
selected server is free is less than (1 -  ), the
value predicted by the independence argument. Here, discovering that the
first selected server is busy shifts the system state probabilities in
the direction of busier states. One can show that if ), the
value predicted by the independence argument. Here, discovering that the
first selected server is busy shifts the system state probabilities in
the direction of busier states. One can show that if
then Q(N,  , j) is a monotonically
decreasing function of j; otherwise, it is a unimodal function of
j, reaching a minimum for some value of j, say
jo, and then increasing for all j greater than
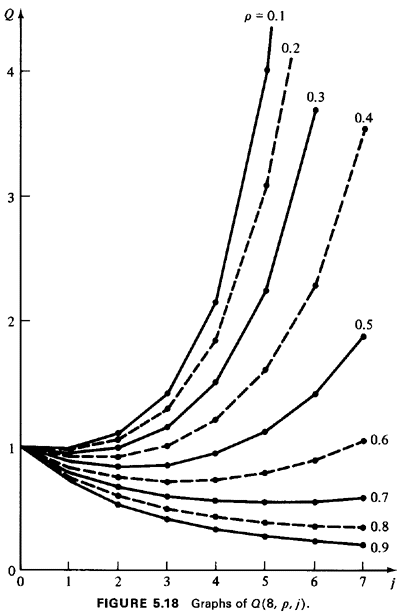
jo. For illustrative purposes, plots of Q(8, , j) is a monotonically
decreasing function of j; otherwise, it is a unimodal function of
j, reaching a minimum for some value of j, say
jo, and then increasing for all j greater than
jo. For illustrative purposes, plots of Q(8,
 , j) are given in Figure 5.18. , j) are given in Figure 5.18.
Even though the correction factor Q(N,  ,
j) was derived assuming homogeneity of servers, one could conjecture
that the same factor could be used as an approximation in an M / M /
N system with distinguishable servers. This would seem especially
appropriate for systems in which the workloads of servers do not differ
too greatly and in which many different dispatch preference vectors
(motivated by different customer locations) effectively simulate in the
aggregate "blindfolded" selection of servers. Implementing this
conjecture has yielded numerical results that are typically within 1 or
2 percent of the exact "hypercube" results. ,
j) was derived assuming homogeneity of servers, one could conjecture
that the same factor could be used as an approximation in an M / M /
N system with distinguishable servers. This would seem especially
appropriate for systems in which the workloads of servers do not differ
too greatly and in which many different dispatch preference vectors
(motivated by different customer locations) effectively simulate in the
aggregate "blindfolded" selection of servers. Implementing this
conjecture has yielded numerical results that are typically within 1 or
2 percent of the exact "hypercube" results.
|



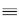 event that jth
selected server is busy (not available)
event that jth
selected server is busy (not available)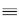 BjC = event that jth server selected
is free (or available)
BjC = event that jth server selected
is free (or available)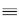 probability that the first free server is the
(j + 1)st server selected
probability that the first free server is the
(j + 1)st server selected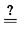
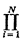
 si
si , j) =
, j) =