5.5 HYPERCUBE APPROXIMATION PROCEDURE
(INFINITE LINE CAPACITY)
As just discussed, the storage and execution time required to solve
the hypercube model equations roughly doubles with each additional
server. Thus, one is motivated to find an efficient approximation
procedure that computes to reasonable accuracy all the hypercube
performance measures. Such a procedure has been developed that requires
solution to only N simultaneous equations rather than
2N, as in the exact model [LARS 75a].
The approximation has been found to compute results to within 1 or 2
percent of the exact results. In most practical situations such
approximate solutions should suffice. For instance, data inaccuracies
may not justify use of a highly precise model. Or the system planner may
not have access to a sophisticated computer system necessary to perform
calculations with the exact model. Or certain nonquantifiable concerns,
perhaps involving political, legal, spatial, or administrative
constraints, may play an important role in system design, thereby making
precise estimates of quantifiable performance measures unnecessary.
Finally, the approximation procedure can be carried out on a computer
for any reasonable number of servers N, whereas the exact model
is impractical for N greater than 15.
In this section we will simply sketch out the key ideas of the
approximation procedure, as applied to the basic infinite queue capacity
hypercube model of the previous section. Full details are found in [LARS
75a]. In complex urban service systems, we expect such approximations to
play an increasingly important role in bringing computationally
practical models to the aid of the urban decision maker.
The following are the main features of the approximation
procedure:
- As with the exact model, one assumes that the dispatcher has a
rank-ordered list of preferred units to dispatch to service requests
from each geographical atom and that he always dispatches the most
preferred available (free) unit (i.e., fixed-preference dispatching).
- In addition, if
 n is
the fraction of time that unit n is busy, we use (1 - n is
the fraction of time that unit n is busy, we use (1 -  n) as the probability that unit
n will be available to be dispatched to a service request when
all units more preferred than unit n are busy. A correction factor is
used as a multiplier to make this approximation as exact as possible.
For instance, if unit 5 is the third preferred for a particular request,
and units 7 and 2 are preferred to unit 5, the probability that unit 5
will be dispatched is equal to n) as the probability that unit
n will be available to be dispatched to a service request when
all units more preferred than unit n are busy. A correction factor is
used as a multiplier to make this approximation as exact as possible.
For instance, if unit 5 is the third preferred for a particular request,
and units 7 and 2 are preferred to unit 5, the probability that unit 5
will be dispatched is equal to  7 7  2 2 (1 - (1 -  5) 5) (correction factor). (correction factor).
- The correction factor, which can deviate significantly from 1, is
derived to account for the fact that the statuses of servers are not
independent (as would be assumed if the correction factor were always
1).
- Given features 2 and 3, we can write N simultaneous
equations relating the N unknowns (the workloads) to the dispatch
policy and the arrival rates from the various geographical atoms.
- The N simultaneous equations are solved iteratively,
thereby yielding estimates of the workloads of the units.
- If we desire other performance measures of the system (e.g., the
mean travel time to each geographical atom or the fraction of dispatches
that are interresponse area), then the values of the utilization factors
found in feature 5 may be used to estimate the fraction of dispatches
that send unit n to atom j, for all n and j.
These fractions are then entered into simple equations to obtain
estimates of the values of the desired performance measures.
The derivation of the approximation procedure is carried out assuming
the M / M / N infinite-capacity model with indistinguishable
(homogeneous) servers. As usual, the arrival rate is 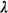 , the mean service time (for each server) is , the mean service time (for each server) is 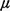 -1, and -1, and  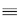 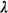 N N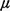 < 1. The approximation arises from the fact that in
the context of an urban service system, the servers are distinguishable
and thus have differing performance characteristics. < 1. The approximation arises from the fact that in
the context of an urban service system, the servers are distinguishable
and thus have differing performance characteristics.
|


