|
5.1 M / G / 1 modified queue Apply (5.2) for the case
of a rectangular (Xo-by-Yo) service
region with directions of travel parallel to the sides of the rectangle
and with a single emergency repair unit garaged at the region's center,
(x = Xo/2, y = Yo/2). The
emergency repair unit operates as in the third paragraph of Section
5.2.
- Suppose that
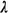 = 1 call per hour. Let us
examine how several alternative service region designs having equal area
(i.e., XoYo = A) can affect system
performance. Let A = 4 square miles and response speed be 10
miles/hr. Further, suppose that the mean and variance of on-scene
service time are 45 minutes and (45)2 minutes2,
respectively. Find the mean time from calling until arrival of a service
unit for Xo = Yo,
Xo= 2Yo, and Xo =
20Yo (assuming that we constrain
XoYo = A = 4 square miles). Can the
system be saturated (i.e., = 1 call per hour. Let us
examine how several alternative service region designs having equal area
(i.e., XoYo = A) can affect system
performance. Let A = 4 square miles and response speed be 10
miles/hr. Further, suppose that the mean and variance of on-scene
service time are 45 minutes and (45)2 minutes2,
respectively. Find the mean time from calling until arrival of a service
unit for Xo = Yo,
Xo= 2Yo, and Xo =
20Yo (assuming that we constrain
XoYo = A = 4 square miles). Can the
system be saturated (i.e., 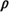 > 1) for some values
of Xo, Yo, and unsaturated for
others? > 1) for some values
of Xo, Yo, and unsaturated for
others?
- Verify that with the constraint XoYo
= A, minimum response time is always achieved by setting
Xo = Yo =
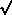 A A
|


