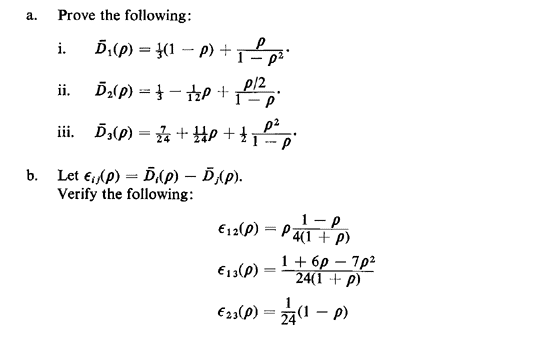|
5.2 Infinite array of linear concatenated sectors One
infinite server spatially distributed queueing system that has provided
certain physical insights into alternative dispatching procedures is a
linear concatenated sector system. On the x-axis, assume that
sector i covers the interval from x = i/2 to
x = (i/2) + 1 for i even and from x =
-(i + 1)/2 to x = -(i - 1)/2 for i odd.
Response unit i is assigned to patrol uniformly sector i
when it is available for dispatch assignment. Each unit is assumed to be
available with probability (1 - 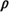 ),
independently of the status of all other units. (It should be
clear that the independence assumption is an approximation.) The
position of each available unit is selected from a uniform distribution
over the length of the unit's sector. The random variable indicating the
position of unit i is Xi; a particular
experimental value of the random variable is xi. ),
independently of the status of all other units. (It should be
clear that the independence assumption is an approximation.) The
position of each available unit is selected from a uniform distribution
over the length of the unit's sector. The random variable indicating the
position of unit i is Xi; a particular
experimental value of the random variable is xi.
Assume that an incident is reported from some point x in
sector 0 (0 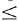 x x 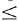 1) and that the dispatcher must select an
available unit to assign to the incident. The incident position x
is drawn from a uniform probability density over [0, 1]. The dispatcher
may use any one of the following three selection criteria: 1) and that the dispatcher must select an
available unit to assign to the incident. The incident position x
is drawn from a uniform probability density over [0, 1]. The dispatcher
may use any one of the following three selection criteria:

Let 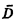 i( i(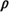 ) = expected travel distance for strategy i,
given a utilization factor of ) = expected travel distance for strategy i,
given a utilization factor of 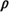 (i = 1, 2,
3). (i = 1, 2,
3).
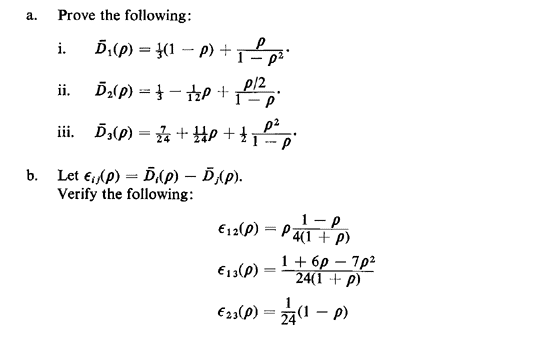
Do these results make intuitive sense for limiting values of 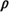 ? What practical significance do they have? ? What practical significance do they have?
|