|
5.16 Linking travel times infinite regions to spatial
Poisson
processes In this problem we wish to explore the validity of
the spatial Poisson process model as we increase the number of
independently, uniformly located response units in our
area.
- If a unit n is uniformly distributed over a square region
of
area N and if the incident is located at the center of the
square,
find the probability density function of Dn, the
travel distance for unit n to reach the incident. (Assume that we
have
right-angle response parallel to the sides of the square.)
- Assume that there are N such units in the region, indexed
from
n = 1 to n = N. The minimum travel time to an
incident is
RN = Min [D1, D2,
. . ., DN]
But the spatial Poisson assumption implies that as N gets large,
the pdf for RN approaches a Rayleigh with parameter 2.
The cumulative distribution function for a Rayleigh random
variable with parameter 2 is
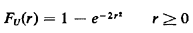
Thus, if the spatial Poisson model is correct for large N, we
must have
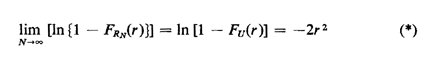
Prove (*).
- Explain briefly how your analysis in part (b) is modified if
you do not condition on the position of the incident being at the center
of
the square.
- How might we use this result in developing an approximate model
for travel time in a finite homogeneous region with
N response units, demand rate
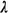 (incidents/hour), average service time
(incidents/hour), average service time 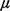 -1, and a service discipline that assigns
units completing service to the closest waiting call ? -1, and a service discipline that assigns
units completing service to the closest waiting call ?
|


