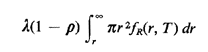|
5.17 Coverage problem for urban service systems
Consider a
collection of response units in the plane whose positions are
distributed according to a spatial Poisson process with parameter
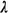 A(S), where A(S) denotes the
area of the region S. Each unit is available for dispatch with
probability (1 - A(S), where A(S) denotes the
area of the region S. Each unit is available for dispatch with
probability (1 - 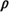 ), independent of the status of
all other units. Units have different response speeds: the (Euclidean)
distance that a randomly chosen available unit can travel in a time
T is determined by the probability density function
fR(r, T) (T fixed). Show that the number of
available response units which can travel to a random
incident in the time T is a Poisson random variable with
parameter ), independent of the status of
all other units. Units have different response speeds: the (Euclidean)
distance that a randomly chosen available unit can travel in a time
T is determined by the probability density function
fR(r, T) (T fixed). Show that the number of
available response units which can travel to a random
incident in the time T is a Poisson random variable with
parameter
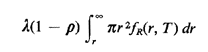
Hint: Define the family of random variables C(r, T)  the number of available response units that can
get to an incident in
time T and that are located at a distance less than r from
the
incident. Show that the family C(r, T) determines a time-varying
Poisson process where the time variable is taken to be the
distance r. To do this, prove that a "Poisson event" occurring in
a ring between r and r + dr centered at the
incident has
probability the number of available response units that can
get to an incident in
time T and that are located at a distance less than r from
the
incident. Show that the family C(r, T) determines a time-varying
Poisson process where the time variable is taken to be the
distance r. To do this, prove that a "Poisson event" occurring in
a ring between r and r + dr centered at the
incident has
probability 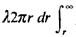 fR(x, T)
dx, and
events occurring over disjoint intervals constitute independent
random variables. Then show that C(r, T) is a variable-time
(nonhomogeneous) Poisson process with parameter fR(x, T)
dx, and
events occurring over disjoint intervals constitute independent
random variables. Then show that C(r, T) is a variable-time
(nonhomogeneous) Poisson process with parameter
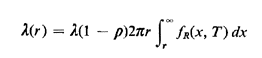
|