|
5.5 More on the square-root law We wish to explore the
reasonableness of the approximation E[1/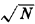 ] ] 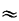 1/ 1/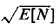 . We know from Section 5.8 that, in fact,
E[1/ . We know from Section 5.8 that, in fact,
E[1/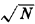 ] > 1/ ] > 1/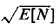 . .
- Suppose that N is uniformly distributed over the integers
1, 2, . . . , 10. Verify that
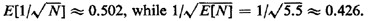
- Now suppose that N's distribution is clustered more around
its mean:
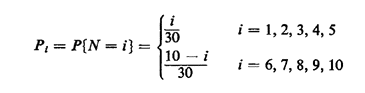 Verify in this case that E[1/
Verify in this case that E[1/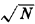 ] ] 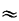 0.466, a result much closer to the desired
approximation. 0.466, a result much closer to the desired
approximation.
- Now suppose that E[N] is large and N's
distribution is fairly symmetric about its mean E[N],
which for simplicity we assume to be an integer. Using the square-root
approximation
(y +
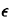 ) ) 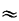 y-½ + ½ y-½
y-½ + ½ y-½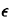 for |
for |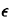 | considerably smaller than y >
0, write E[1/ | considerably smaller than y >
0, write E[1/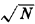 ] as a series of terms
symmetrically expanded about the mean ] as a series of terms
symmetrically expanded about the mean
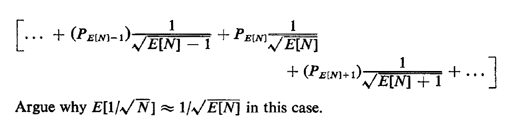
|


