


|
5.6 Ring city Consider a ring city of circumference 6 miles which is serviced by three emergency response units. When not servicing an emergency call, a response unit is stationed at its "home location," located at the middle of the unit's district. There are three home locations (and districts) positioned symmetrically around the city as shown in Figure P5.6. Calls for service occur as a homogeneous Poisson process (in time) at average rate two calls per hour. Locations of calls are uniformly, independently distributed over the circle's circumference. The total service time per call is negatively exponentially distributed with mean 1 hour. Travel time can be ignored when computing service times, since units respond (traveling along the circle) at 60 miles/hr (1 mile/min). 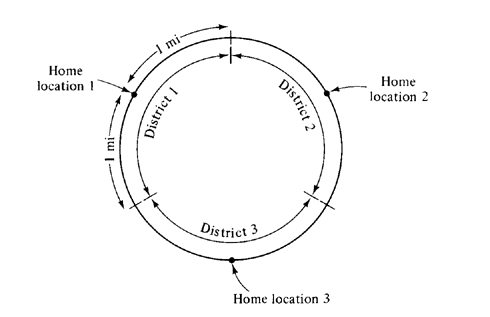
The dispatching strategy is as follows for a call from district i (i = 1, 2, 3):
As soon as a unit has completed servicing a call, we assume that it returns nearly instantaneously to its home location (even if it is then dispatched to a call waiting in queue). Assume that the system is operating in the steady state.
|