


6.3.1 Solving the MST ProblemThe solution of MST problems turns out to be very simple. Of the several efficient algorithms that have been proposed for it, some are more useful for manual computations and others more suitable for computer applications. All the algorithms derive their validity from the following property of minimum spanning trees. Fundamental property of MST's. Suppose that a procedure
for finding the MST of any graph G has been discovered and that in the course
of the construction of the MST, by using this procedure, the set N of nodes
of G has been partitioned into k distinct trees T1(N1,
A1), T2(N2 A2), ...,
Tk(Nk, Ak) with N1
Proof: (By contradiction) Assume that (i*, j*) is not part of the final MST, which, however, must, by assumption, contain both the tree Ts and the tree Tt. By definition of the MST, there is exactly one path leading from Ts to Tt. Let then (i, j) be that link on the MST which has one of its roots, i, in Ts and the other, j, not in Ts and which is the first link on the path from Ts to Tt (It is possible that i = i* or that j = j*.) By definition of (i*, j*), l(i, j) > l(i*, j*). If we then replace (i, j) by (i*, j*), a new spanning tree will result which will have less total length than the MST--a contradiction. Note that in stating the property above we did not make any specific assumptions about the procedure for constructing the MST. We can then begin the procedure with n trees (where n is the number of nodes in the set N), with each tree consisting of a single isolated node and no links. We can then, according to the property that we proved, connect any arbitrarily chosen tree (node) to its nearest tree (node) and continue this procedure until all nodes are finally connected. Before proceeding to describe the details of this algorithm, we state the following corollary to the fundamental property of the MST's that we have proven: Corollary: In an undirected network, G. the link of shortest length out of any node is part of the MST. Proof: Follows directly from the fundamental property of MST's. This corollary can be used to speed up the algorithmic procedure outlined below. However, it will not be explicitly included here. MST Algorithm (Algorithm 6.3)
Obviously, the most time-consuming of our MST algorithm's steps is the one that involves finding the next node to be included in the MST. This, in effect, means comparing the lengths of all links leading from nodes already included in the MST to nodes not included in the MST to find the shortest one. Repeated application of this step is computationally expensive. To overcome this problem, an alternative algorithm calls for the ranking of all links in G according to length and then the addition to the MST at each stage of the shortest link such that no cycle is formed with previously chosen links. Unfortunately, this approach also suffers from a computational disadvantage: checking for cycles--a trivial task in the case of manual solutions--is nontrivial in the case of computer applications and becomes "expensive', for large problems. Finally, we note that whenever, in the course of applying Algorithm 6.3, a tie arises (and is broken arbitrarily), this raises the possibility that two or more minimum spanning trees of the graph G exist. Although the total length of all of these tied MST,s will be the same, they may differ markedly from each other in terms of which links each of them includes. Exercise 6.2 Show that Algorithm 6.3 can be executed in O(n2) time.
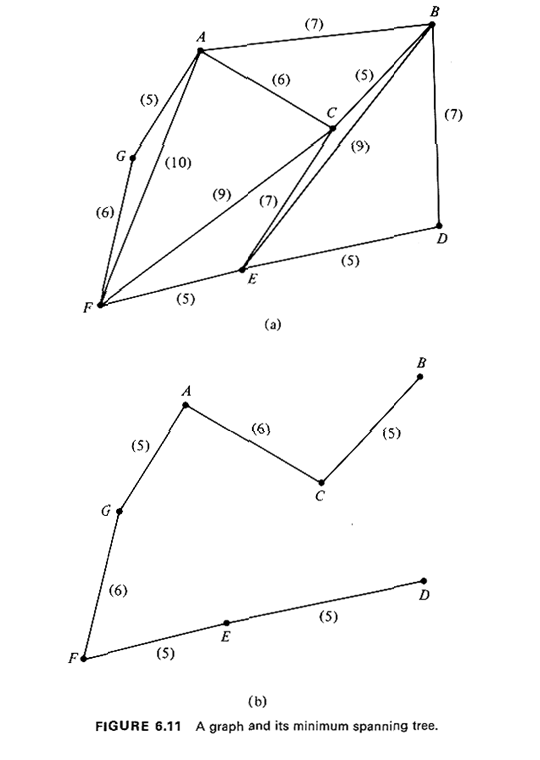
9 The algorithm assumes n |