


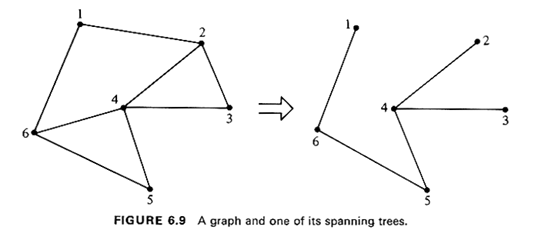
6.3 MINIMUM-SPANNING-TREE PROBLEMA spanning tree of an undirected graph G(N, A) has already been defined as a tree of the graph G that contains the complete set of nodes, N, of G (see also Figure 6.9). The minimum-spanning-tree problem is then concerned with finding the one among all possible spanning trees of a graph G(N, A) with the minimum total link length. If the number of nodes in the set N is n, then all spanning trees of G obviously contain n - 1 links. Just as in the case of shortest-path problems, the minimum-spanning-tree
(MST) problem has direct applications of its own, primarily in problems of
transportation network design, and also constitutes an important building
block in some solution approaches to other more complex problems such as
node-covering problems (see Section 6.4). For a brief example of an
application of the MST problem, consider the case in which map locations
of n rural towns are given along with a matrix listing the Euclidean
distances (or some other measure of distance, time, or cost) between all
possible pairs of towns. The MST can be interpreted in this case as the
minimum length of roads needed to connect, directly or indirectly, all
pairs of towns, assuming that all road segments (links) begin and end in
some pair of towns.
The last sentence emphasizes the distinction between the MST problem
and the so-called "Steiner problem." The latter has the same objective
as the former but allows the introduction of artificial "nodes" (i.e.,
links can meet anywhere on the plane instead of only at the specified
points that are to be spanned). To illustrate this further, consider
four towns that lie at the corners of a unit square. Obviously, one solution
to the MST problem in this case is the one shown in Figure 6.10a; the
total length of the minimum spanning tree is 3 units. On the other hand,
it can be shown that if creation of artificial nodes is permitted
(Steiner,s problem), the total line length needed to connect the four
points can be further reduced. The solution to Steiner's problem in this
case is shown in Figure 6.10b and involves creation of two artificial
nodes (A and B in Figure 6.10b); the total length of the Steiner tree is
1 + 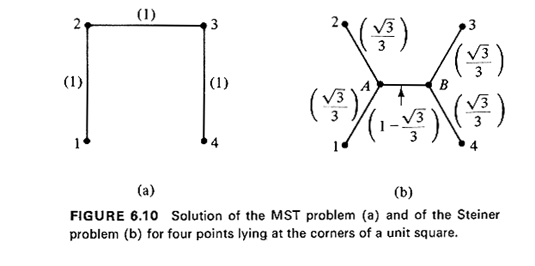
|