


6.4.11 m-TSP ProblemKeeping in mind that the m-traveling salesmen problem is, by definition, a single origin-destination problem, it can be easily shown that it can be reformulated as a classical TSP with little effort. Thus, the m-salesmen problem is no more difficult than its one-salesman counterpart, as measured by worstcase computational complexity. (Interestingly, this simple observation was not made until 1973 and 1974 in several independently published papers [BELL 74, ORLO 74, SVES 73].) Suppose that a m-TSP is given with n points to be visited and with all
tours beginning and ending at a common origin V. [Were m = I we would thus
have a (n + I)-node TSP.] The equivalent formulation is then obtained by
replacing the origin V by m exact copies of it, Vl,
V2, . . . , Vm each connected to the other n nodes
exactly as was the original origin and with the same distances. That is,
if x is any one of the n points to be visited, then However, the links connecting the m copies of the origin to each other
are assigned "infinite" length, that is, very large by comparison to all
other distances in the problem [d(Vi, Vj) =
If we now solve this as a classical single-salesman, (m + n)-point TSP, it can be seen that a minimum tour will never use a link connecting two copies of the origin. In other words, in the shortest single-salesman tour, the sequence "Vi followed by Vj" will never appear (i, j = 1, 2, . . . , m). Then, if the (m + n)-point, single-salesman tour is "folded back" by merging together all copies of the origin into a single node V, the single-salesman tour will decompose into m tours as required by the m-TSP. Example 12: Two-Salesmen Problem 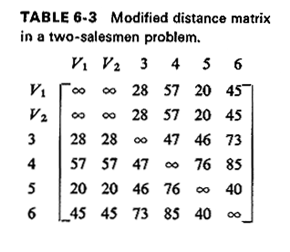
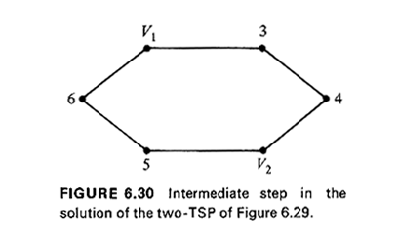
With regard to the solution of the m-TSP problem, it should be noted that, theoretically, the "MST-and-matching" heuristic algorithm that we presented earlier (Algorithm 6.6) is not applicable, even when the original distance matrix is symmetric and satisfies the triangular inequality. The reason is that, because of setting the distances between the copies of the origins to infinity (or to a "very large" number), the expanded matrix--with the m - 1 copies of the origin--does not satisfy the triangular inequality. In practice, however, if one is careful, the algorithm still can be applied with success (in the great majority of cases) to obtain a single TSP tour with the expanded matrix. The only cases when the algorithm fails occur when more than half of the odd nodes of the minimum spanning tree on completion of Step 1 of Algorithm 6.6 are nodes that correspond to copies of the origin. This, in turn, would mean that in matching odd degree nodes (Step 2) we would be forced to match two copies of the origin to each other--leading to a tour of infinite length. We conclude our discussion of the m-TSP by noting that, irrespective of
whether or not the original distance matrix satisfies the triangular
inequality,
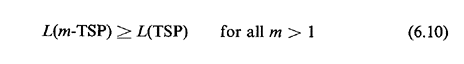
where L(m-TSP) and L(TSP) are, respectively, the lengths of the
optimum m-salesmen and single-salesman tours for any given problem.
To see the validity of (6.10) simply note that the m-TSP tour has been shown
here to cover m - 1 points in addition to the original n + 1 that the 1-TSP
tour covers. In fact, we have shown by construction that, more generally,
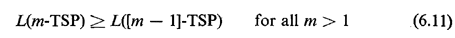
|