6.4.13 Multidepot VRP

The existence of multiple depots (or multiple origins in unconstrained, traveling-salesman-type problems) poses the additional requirement of assigning demand points to specific depots. This new "degree of freedom" further increases the computational complexity of the problem.

The approach to multidepot VRP problems so far has been based entirely on heuristic algorithms, of which the most common are of the "cluster first, route second" variety: first, demand points are assigned to depots; then, single depot VRP's are solved for each depot.

The best known of these approaches [GILL 74a] assigns demand points to depots in the following way: For each demand point i, we compute the quantity

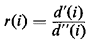
where d'(i) and d''(i) are the distances from i to the nearest and second nearest of its depots. A threshold value such that 0 < < 1 is specified next and compared to each r(i). if r(i) , then the demand point i is immediately assigned to its nearest depot. however, if r(i) > , then the demand point is reserved for more careful consideration. After all points i such that r(i) have been assigned to depots, and therefore clusters have been formed around the depots, points with r(i) > are processed again: if two points j and k have already been assigned to a given depot, say depot D_s, then inserting point i between nodes j and k on a route originating (and terminating) at D_s, increases the length of that route by d_jk(i) = d(j, i) + d(i, k) - d(j, k). Point i is then assigned to the depot associated with the minimum of the quantities d_jk(i), for all pairs of points (j, k) already assigned to a depot. When all demand points have been assigned to a depot in this manner, a single-depot VRP algorithm can be used to design the vehicle routes.

An extension of the savings algorithm to multidepot VRP's that avoids the early partitioning of the demand points into clusters around depots has also been developed [TILL 72]. The latter algorithm has been recently combined with the cluster-forming approach outlined above into an efficient algorithm capable of handling large-scale problems [GOLD 76].