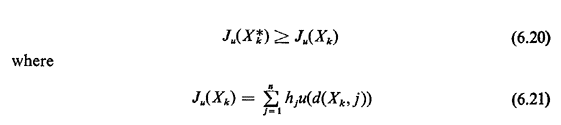6.5.3 Generalization and Extensions
Since Hakimi's theorem first appeared, that very powerful result has
been considerably generalized. The most general version [LEVY 67] defines
optimal k-medians as follows:
Definition: Let u(d(x, y)) be a function representing the utility of covering
the distance d(x, y) on a network G. Then, a set of k points X*k
on G is a set of optimal k-medians of G if, for every Xk 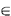 G
G
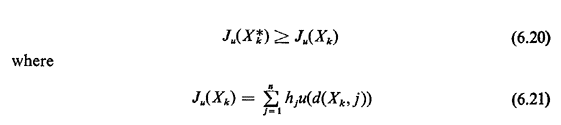
In words, the optimal medians maximize the total utility associated with
the travel by all service users of the k facilities. The following theorem
has then been shown to be true:
Theorem: At least one set of k-medians exists solely on the nodes
of G as long as the utility function u(·) is a convex function
of the distance d.
Several other results applicable to practically significant extensions of the basic k-median problem are also available.
Example 16: Locating Supplementary facilities on an Urban Network
It often happens, particularly with regard to urban transportation
services, that important service facilities in a given area are severely
congested due to high demand. It may then be deemed desirable to establish a
number of secondary facilities, whose sole purpose is to "preprocess" the
prospective users of the primary facilities. Those users who choose
(or, for that matter, are compelled) to pass through the secondary
facilities first, presumably receive some type of "reward" either in the
form of faster access to the primary facilities or in the form of faster
service once they get there or both. A good example of this type of setup
is the often-discussed concept of constructing secondary remote terminals
for airports where prospective air passengers will congregate, will go
through the check-in procedures, and will then be transferred to the
airport. Elaborate plans for this type of system have been drawn up for
several major cities (as, for instance, the plans for high-speed links
between a terminal on Manhattan and the Kennedy and LaGuardia airports in
New York, or between a terminal in downtown London and its contemplated
third airport).
Problems such as these, in which primary facilities already exist
(and quite often are less than optimally located) and secondary facilities
must be established to provide supportive services, are known as
"supporting facility" problems. When the location of the supporting
facilities must be determined so as to minimize the average travel
distance (or time or cost) to all users, then, by analogy to all the above,
we have the "supporting k-medians" problems. It can be shown [MIRC 79a] that
supporting k-medians are optimally located on nodes, irrespective of the
locations of primary facilities, as long as the utility of travel is a
convex function of travel distance (time, cost). Problem 6.10 provides a
detailed example for this type of case.
All that has been said so far on median problems was with reference to
undirected graphs. With a few modifications (and some changes in the
definitions), essentially the same results could have been obtained for
directed graphs (i.e., for cases where some or all of an area's
transportation links are used for one-way travel). It is important to
realize that, with directed graphs, it makes a difference whether the
average distance to be minimized is the distance to the facilities,
from the facilities, or the round-trip distance. In fact,
the distinction is made in the literature between inward medians
(minimize travel to the facilities), outward medians (minimize travel
from the facilities), and simply medians (minimize total
round-trip travel) [MIRC 79b]. While optimal locations for these three cases
will be identical for undirected networks, this will generally not be the
case for directed networks.
Finally, we note that Algorithms 6.10 and 6.11 can be used, with minor
modifications, for the solution of all the problems discussed in this section.
|