


6.5.4 Center ProblemsExample 17: Locating a Firehoase in a Ruwral Area Consider the graph shown on Figure 6.37 which depicts a rural area with
five towns, shown as nodes A through E, connected by a rather sparse
transportation network with link lengths in miles also indicated. Town
populations in thousands are listed in parentheses next to each node.
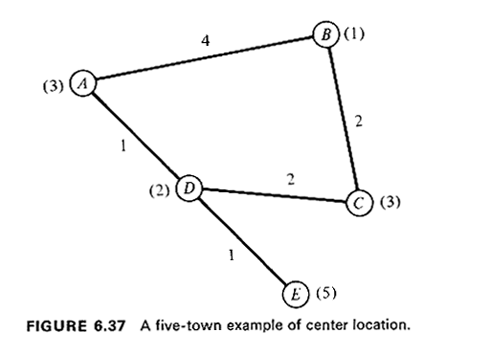
The towns have entered into a cooperative agreement to obtain joint fire protection for certain types of fires. They are planning to build a firehouse where a single special, purpose fire engine, yet to be purchased, will be stationed. A considerable amount of discussion has led to the conclusion that the location of the firehouse must be such as to minimize the farthest distance that the fire engine will ever have to travel in responding to a fire alarm. This, indeed, is a quite reasonable objective for an emergency-type service such as the fire department. Suppose, first, that the location of the firehouse were restricted to be
at one of the five cooperating towns. By first obtaining the minimumdistance
matrix [d(i, j)] for the given network and then by choosing the row with the
minimum maximum entry, we can find the node that minimizes the maximum
distance to all other nodes. This procedure is shown in Table 6-10. The
optimum location for the facility is town C with a maximum distance of 3
miles to both town A and town E.

Then let us ask whether the unrestricted optimum location for the firehouse is also on node C. That is, if we are free to locate the firehouse at any point at all on the network, will it still be located at town C? This turns out to be a rather difficult question to answer. We shall do this after introducing a convenient notation and some definitions. Let G(N, A) be an undirected network. (Entirely similar concepts with
some minor modifications to account for link directivity apply to directed
networks.) Let x 
With reference to our last example, we have already found the vertex center of the graph of Figure 6.37 to be at node C. We now wish to find the absolute center of that graph. An algorithm for finding the absolute center of an undirected graph G can be simply described as follows. Single-Center Algorithm (Algorithm 6.12)
Unfortunately, Step 1 of this simple two-step algorithm is a time-consuming one. We illustrate this through our earlier example.
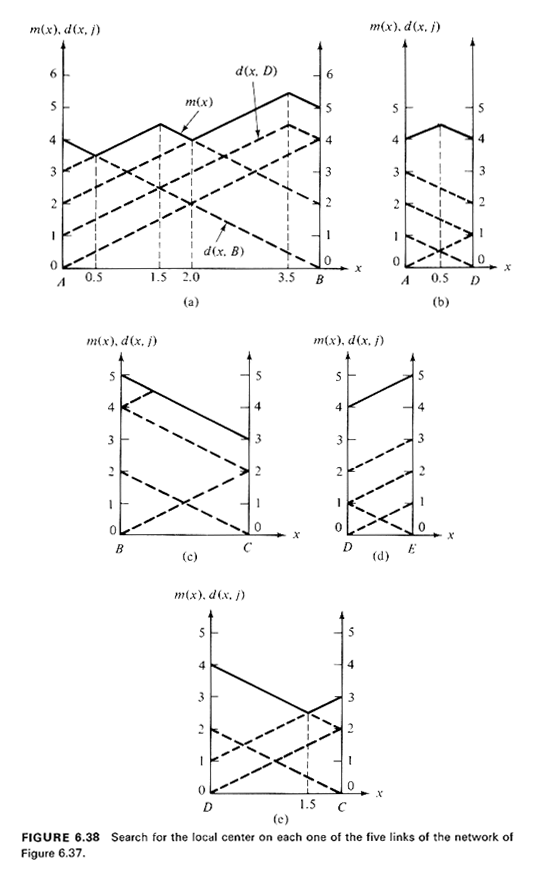
Consider, for instance, the link (A, B) with a length of 4 units. For
all points x on (A, B) we can find and plot the functions d(x, j) for
j = A, B. C, D, E. For instance, if we set, by convention, x = 0 at A and
x = 4 at B. we have
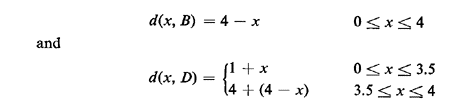
The functions d(x, A), d(x, B), d(x, C), d(x, D), and d(x, E) are all
shown on Figure 6.38a for the link (A, B). Now, since, by definition, the function m(x) is given by the upper envelope for the five functions
as shown on Figure 6.38a. Obviously, the local center of link (A, B) is at a
point 0.5 unit away from A (and 3.5 units away from B) and
m(x Repeating the same procedure for the other four links, we finally obtain
This completes Step 1 of the algorithm. In Step 2 we choose the point x* on the link (C, D) and 0.5 unit away from C for the location of the absolute center; m(x*) = 2.5. From our example we conclude that:
From the second remark above, the following result can be easily derived [ODON 74]: Theorem: For the local center, x 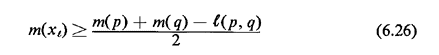
where, as usual, 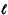 (p, q) denotes the length of link (p, q). (p, q) denotes the length of link (p, q).
Exercise 6.7 Prove the validity of the theorem. From this theorem and from the observation that, by definition,
m(i*) If for a link (p, q),
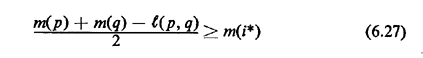
then the local center x This test, taking advantage of the fact that it is very simple to find m(i*), often leads to considerable reduction in the computation effort required to obtain the absolute center (see also Problem 6.12).
We also note that a highly efficient algorithm exists for finding the absolute center when the network at hand happens to be a tree (see Problem 6.11). The algorithm [HAND 73] is the following: Single-Tree-Center Algorithm (Algorithm 6.13)Let G be a tree network and let ei (i = 1, 2, . . ., m) represent the end vertices (i.e., the nodes of degree 1) of the tree. Then:
This last algorithm does not even require computing the minimum distance matrix for the tree network G! |