6.5.7 Set-Covering Problems
Another subproblem that often arises in connection with solving
requirements problems is known as the set-covering problem. It can be
described as follows.
Consider a set Yn = {y1, y2, . . .,
yn} of n points on a network G (for instance, Yn
could be the set of demand-generating nodes on G) and another set
Xm = {x1, x2, . . ., xn} of
m points on G which are candidates for the location of a set of facilities
(some of the points in Xm may coincide with points in
Yn). Let us now assume that an unambiguous threshold of
performance (e.g., a maximum distance 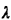 ) has been specified
so that any
location xj ) has been specified
so that any
location xj 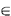 Xmm
can be viewed as either satisfying
or falling short of achieving that level of performance with respect to any
point y1 Xmm
can be viewed as either satisfying
or falling short of achieving that level of performance with respect to any
point y1 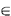 Yn. Then
we say that a point xj Yn. Then
we say that a point xj
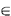 Xm "covers" ("does not cover") a point yi Xm "covers" ("does not cover") a point yi
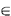 Ynif the point xj satisfies (does not satisfy) the
threshold of performance with respect to point yi. For instance,
when the threshold of performance is a maximum distance
Ynif the point xj satisfies (does not satisfy) the
threshold of performance with respect to point yi. For instance,
when the threshold of performance is a maximum distance 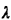 , then
xj covers yj if d(xj, yi,) , then
xj covers yj if d(xj, yi,) 
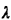 and does not cover it if d(xj, yi) >
and does not cover it if d(xj, yi) > 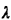 . The
similarity with the concepts of coverage in Section 3.6 is obvious. . The
similarity with the concepts of coverage in Section 3.6 is obvious.
The set-covering problem then consists of finding the minimum number,
say k*, of points from the set Xm such that all
points in Yn are covered.
Example 19: Sef-Covering Problem
Consider seven urban locations A through G and five distinct points V
through Z in the same urban area. All 12 points lie on an urban road network.
We shall call the points A through G the "demand set" of this problem and
points Vthrough Z the "facilities set." We wish to find the smallest number
of points in the facilities set needed to cover the demand set of points if
it is specified that each point in the demand set must be within 20 minutes
of travel distance from a point in the facilities set. The 5 x 7 matrix of
minimum distances (in minutes) on the network is given in Table 6-11.

The minimum distance matrix [d(i, j)] can immediately be translated into
the coverage matrix, tC(i, j)], by setting each matrix element c(i, j) to

The coverage matrix for our problem is shown in Table 6-12. Potential
facility point W. for example, can cover demand points C, D, and G.
The set-covering problem (SCP) can now be stated simply as follows.
Reduce the coverage matrix [c(i, j)] to the minimum number of rows required
so that each column in the reduced matrix has at least a single element
equal to 1. The problem in this form can be readily formulated as an integer
programming 0-1 problem, and indeed the best-known approaches to it
[GARF 72, TORE 71] begin with such a formulation and develop general
algorithms for the solution of SCP's.
Here we shall not describe these general algorithms. We shall outline
instead a very simple matrix-reduction algorithm which may be used to reduce
the computational size of SCP's. In many cases, especially those involving
facility location problems on urban or rural roadway networks, this
matrix-reduction algorithm simplifies SCP's so much that a solution can
e obtained by inspection upon completion of the reduction process.
Matrix Reduction for Set Covering (Algorithm 6.14)
| STEP: | 1
| (Feasibility Check): If there is at least one column in the
coverage matrix that consists entirely of zeroes, stop. No feasible
solution exists (i.e., the performance standards for coverage must be relaxed
or more points must be added to the facilities set).
| | STEP: | 2
| If any columns have only one nonzero element, say in
row i*, then the point corresponding to row i* must
receive a facility. Include that point in the list of those that must
receive a facility and eliminate row i* and all columns having
a 1 in row i* from the matrix.
| | STEP: | 3 | If
any row(s) i" is such that all its entries are less than or equal to the
corresponding entries of another row i' [i.e., if c(i", j)  c(i',j) for
all j], then eliminate row i". c(i',j) for
all j], then eliminate row i".
| | STEP: | 4
| If any column(s) j" is such that all its entries are
greater than or equal to the corresponding entries of another column j'
[i.e., if c(i,j")  c(i,j') for all i], then eliminate column j". c(i,j') for all i], then eliminate column j".
| | STEP: | 5
| Repeat Steps 2-4 until either (a) the coverage matrix
becomes completely empty or (b) no columns or rows are eliminated during a
complete pass through Steps 2-4. In case (a), a complete solution (minimum
number of facilities and their locations) has been obtained on termination.
In case (b), a solution may be obtainable by inspection on termination, or
application of a more sophisticated SCP algorithm to the reduced matrix may
be necessary.
|
The rationale for each one of Steps 1-5 is rather obvious. The following
example may also be helpful in understanding Algorithm 6.14.
Example l9(continued)
Let us apply Algorithm 6.14 to the set-covering problem already described.
The initial coverage matrix [c(i, j)] is given in Table 6-12. By inspection
we can determine that a feasible solution does exist, since all columns of
[c(i,j)] contain at least a single nonzero entry (Step 1).
In Step 2, we find that column F has only one nonzero element at row X.
It follows that a facility must be located at X to serve, at the
least, demand point F. We eliminate from the coverage matrix row X and
columns A, D, and F [since c(X, A) = c(X, D) = c(X, F) = 1] and obtain the
reduced matrix shown in Table 6-13a.
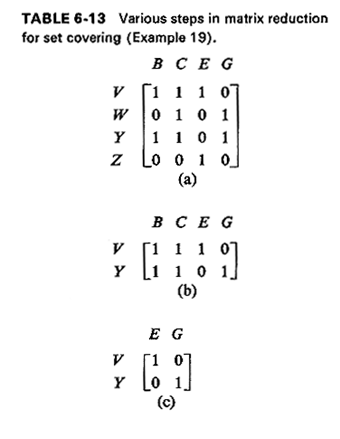
At Step 3, rows W and Z are eliminated (Table 6-13b). All entries of row
W are less than or equal to the corresponding entries of row Y. and
therefore all points covered by a facility at W are also covered by a
facility at Y. The same is true with respect to rows Z and V, respectively.
Next, at Step 4, columns B and C are eliminated since their entries are all
greater than or equal to the corresponding entries of column E (or, for that
matter, G)--hence any facility location that covers demand point Ewill also
cover demand points B and C. The reduced matrix on completion of Step 4 is
shown in Table 6-13c. Finally, on return to Step 2, facilities must be
located at both points Band Y. and the algorithm terminates since upon
elimination of these two rows, the coverage matrix is empty.
Thus, the minimum set of locations consists of points V, X, and Y. We
may now, if we wish, return to the original minimum distance matrix
[d(i, j)] (see Table 6-11) and assign each demand point to its nearest
facility. This would assure, in addition to coverage within less than 20
minutes, minimization of average travel distance, as well. In this way,
we assign demands from A and E to V, from D and F to X, and from B. C, and
G to Y.
|


