


6.5.8 Related ProblemsThe three classes of facility location problems on networks that we have reviewed here (medians, centers, and requirements problems) are not only important in themselves but also illustrate the basic techniques for approaching a wide variety of related classes of problems. Two examples of such problems follow. The first is concerned with locating so-called "obnoxious" facilities
that everyone wishes to be as far away from as possible. Garbage incinerators
are one example of this type of facility. Airports (to a much lesser extent)
are another. One instance of such a problem is called the maxian
problem and is concerned with finding a set X*k
of locations on a network so as to maximize the function
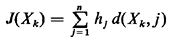
Thus, this problem differs from the median problem only in the fact that it is concerned with maximizing rather than minimizing J(Xk) [CHUR 78]. This, however, requires a very different solution approach than in the case of medians. Our second example is cent-dian problems [HALP 78]. Rather than
have a primary and a secondary objective like the requirements problems,
these problems combine a minisum and a minimax objective into a single
weighted average; that is, they seek to minimize
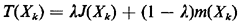
where There is also an almost endless list of variations of requirements (and setcovering) problems, many of which have been motivated by urban applications [TORE 71, GARF 72]. |