


6.6.1 Description and Some Properties of Probabilistic NetworksIt is possible to identify at least three factors that contribute to random variations in travel times on urban roadway networks: (1) random fluctuations in traffic density, traffic lights, and so on, and the attendant variations in travel speeds that result in what could be termed "routine" randomness; (2) changes in the average value of the volume of traffic during hourly, weekly, and seasonal cycles creating "hour-of-the-day" variations in travel times; and (3) accidents, changes in weather conditions, and other unpredictable events causing "nonroutine" randomness. Depending on the context, each one (or combinations) of the randomnessinducing factors above could be the focus of attention in an application. For instance, since decisions on locations of immovable facilities (e.g., a hospital or a firehouse) are of the "strategic" type (i.e., concerned with making a good location choice in the long-term sense), it is variations of the second kind above that one would be particularly concerned with in such cases. That is, we would be mostly interested in the probability distribution of travel times over the course of an average day. This distribution, in turn, can be used as the data base needed to optimize in some sense the accessibility of the facility(ies) over the facility's lifetime. By contrast, when a city is making contingency plans for, say, a major snowstorm, it is randomness of the third kind that is of interest. The planner must estimate accessibility measures on the basis of the likely probability distributions for travel times after the snowstorm (e.g., impassable side streets, traffic jams on main thoroughfares, etc.). No matter what the case is, the representation of (some or all) link lengths as random variables usually means an enormous increase in the computational effort required to answer some of the problems that we solved rather easily earlier for deterministic networks. The main reason is that the shortest distance between any two points on a graph and the associated path are much more difficult to compute or even to conceptualize when link lengths are random variables. Since the computation of shortest distances plays such a fundamental role in most network-based problems, this difficulty extends to the solution of these other problems as well. To see why computation of shortest distances is such a mathematically
cumbersome procedure on probabilistic networks, consider the case of an
undirected graph G(N, A) and the problem of finding the shortest path between
some given pair of nodes s, t 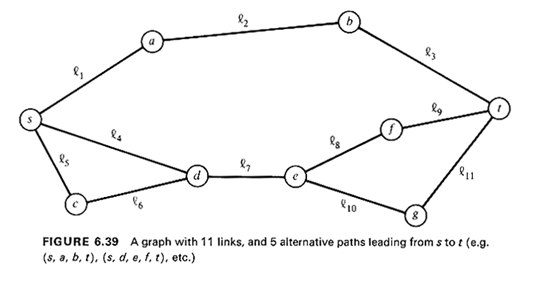
If we now define

Computing the probability distribution for the shortest distance between s and t is thus equivalent to computing the probability density function for the minimum of the q random variables in (6.31). To obtain the probability distribution for D(s,t), FD(s,t)(d), the following steps are therefore necessary:
Obviously, for even a small number of paths, A more mathematically tractable problem is the one concerned with pairwise comparisons of distinct paths. This case arises whenever, in dispatching a vehicle, it is necessary to choose between exactly two given alternative routes on the roadway network. In such cases we can compare the two routes not only with respect to their expected values (which is a trivial matter) but also in a probabilistic sense [FRAN 69]. For example, we may be concerned with guaranteeing that extremely long travel times will be avoided as often as possible. Given two alternative paths (routes) 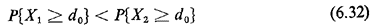
where X1 and X2 are the lengths of When link lengths are statistically independent random variables, the
pdf's for X1 and X2 can be computed through a sequence
of convolutions involving the pdf's of the link lengths for all the links in
each one of the two paths (see also Chapter 2). If, however. the paths
|