


6.6.3 Facility Locations on Probabilistic NetworksAs a further illustration of the application of probabilistic network ideas to urban service system problems, we now reexamine briefly the question of facility location assuming a probabilistic network model. Throughout our discussion we shall be using the discrete and finite state-space model which we described in Section 6.6.2: each probabilistic network can be in one of m states with the probability of it being in state r given by Pr. Two important observations must be made in the beginning:
From the example it is clear that the finest-grained sample space is needed because the shortest path between any two points may vary with the state of the network. In fact, our example also demonstrated that the substitution of expected value E[L(i, j)] for the actual values 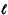 r(i, j) of the
link lengths may lead to erroneous results. Unfortunately, as we noted
earlier, this substitution is often used in practice, since most
deterministic network models are constructed, in the first place, by
using "average" travel times as deterministic substitutes for the random
variables L(i, j) that link lengths really are. Such a substitution may be
justified only when the current state of the network is not known whenever
a trip is started.
r(i, j) of the
link lengths may lead to erroneous results. Unfortunately, as we noted
earlier, this substitution is often used in practice, since most
deterministic network models are constructed, in the first place, by
using "average" travel times as deterministic substitutes for the random
variables L(i, j) that link lengths really are. Such a substitution may be
justified only when the current state of the network is not known whenever
a trip is started.
We now proceed to develop a single-median result for probabilistic networks. For an undirected network G(N, A) with n nodes, we have: Definition: A point x* on an undirected probabilistic
network G is an expected l-median of G. if for every point x
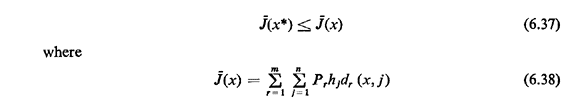
Our result, completely analogous to Hakimi's for deterministic networks, states: Theorem: At least one solution to the expected l-median problem exists on a node in an undirected probabilistic network. This theorem can be proved (see [MIRC 79b]) under the following assumption: Homogeneity assumption: The time required to travel a fraction
The homogeneity assumption states in effect that the speed of travel on any given link is uniform--an assumption that is both straightforward and reasonable since the network model of the urban area can easily be constructed such that this assumption holds. The theorem above can be extended, as one might suspect, to the case of the expected k-medians. In fact, the following even more general result has been shown to hold [MIRC 79b]: Definition: A set of k points X*k on an
undirected probabilistic network G is a set of expected optimal
k-medians of G if for every set Xk 
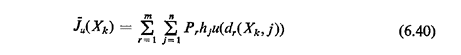
and u(t) is the utility function of travel time t. Then Theorem: At least one set of expected optimal k-medians exists on the nodes in an undirected stochastic network if the utility function for travel time is convex. Similar very general results for medians also apply to directed networks.
Finally, we note that an implicit assumption in the foregoing discussion of
the medians problem on probabilistic networks has been that the appropriate
connectivity conditions apply. For instance, our definition of the expected
single median would be meaningless if it were not true that "those nodes
with nonzero demand (hj > 0) are always, that is, for all m
possible states of the network, connected." Were this not the case, then
some distance(s) between one or more nodes and the facility would be
infinite and so would the expression for The study of probabilistic networks [0n the other hand, the problem of network reliability is a classical one and has been studied extensivelywith reference tocommunications and other networks [FRAN 71].] and their applications to urban service systems has begun in earnest only recently. This is not due to lack of promise of highly useful results but rather to the conceptual and computational difficulties to which we alluded earlier. It can be safely anticipated that this will be one of the most active areas of investigation by operations researchers, management scientists, and others in the next few years. 22 We have shown this to be true for deterministic networks, but we have yet to prove it for probabilistic networks. |