|
6.12 Speeding up the search for the absolute center In our
discussion of the absolutewenter problem, it was pointed out that the quantity
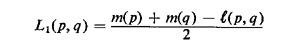
provides a lower bound for the value of m(x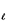 ) on a link (p, q)
[cf. (6.26)]. This bound provides a very convenient test that facilitates
the search for the absolute center of a graph. ) on a link (p, q)
[cf. (6.26)]. This bound provides a very convenient test that facilitates
the search for the absolute center of a graph.
Another bound for m(x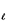 ) has been developed recently, as
follows. For the link (p, q), let r be the farthest node from p (r ) has been developed recently, as
follows. For the link (p, q), let r be the farthest node from p (r
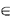 N)
and s the farthest node from q(s N)
and s the farthest node from q(s 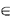 N) [i.e., m(p) = d(p, r) and
m(q) = d(q, s)]. The quantities that will be used to develop the new bound
are d(p, s) and d(q, r). Clearly, the quantity Max [d(x, r), d(x, s)]
provides a lower bound on m(x N) [i.e., m(p) = d(p, r) and
m(q) = d(q, s)]. The quantities that will be used to develop the new bound
are d(p, s) and d(q, r). Clearly, the quantity Max [d(x, r), d(x, s)]
provides a lower bound on m(x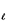 ). ).
| a. | Prove the following result: The
quantity Max{d(x, r), d(x, s)} may attain at most a single local minimum
within (q, p), i.e., excluding the nodes p and q. If such a local
minimum exists it is attained at a point x0 E (p, q) which is
a distance
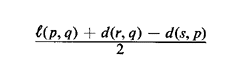
away from node p along (p, q) and at which the value of Max{d(x, r),
d(x, s)} attains the value
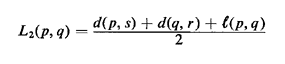
L2(p, q) is then a lower bound for m(x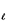 ) for all
points x ) for all
points x 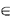 (p, q), excluding the nodes p and q. (p, q), excluding the nodes p and q.
| | b. | Show that L2(p, q) 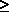 L1(p, q), that is, that L2(p, q) provides a better
lower bound and thus a sharper test than L1(p, q) for speeding up
the search for the absolute center of a graph.
L1(p, q), that is, that L2(p, q) provides a better
lower bound and thus a sharper test than L1(p, q) for speeding up
the search for the absolute center of a graph.
|
|



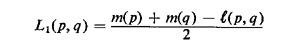
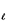 ) on a link (p, q)
[cf. (6.26)]. This bound provides a very convenient test that facilitates
the search for the absolute center of a graph.
) on a link (p, q)
[cf. (6.26)]. This bound provides a very convenient test that facilitates
the search for the absolute center of a graph.