


|
6.13 Facility location with congestion The network of Figure P6.13 represents five towns and the roadways connecting them. Emergency medical centers (one or more) are to be located in this area. The numbers in parentheses indicate the average number of calls for assistance generated per hour at each of the five towns. For each town the call-generating process can be considered Poisson and the process for each town is independent of that for all others. The numbers on the links of the network indicate the travel time, in minutes, for ambulances traveling that link (we assume that travel times within the towns are equal to 0). Assume that it has been decided to locate exactly two medical facilities in this region. Each medical facility will be assigned a set of towns that it will serve exdusively (the two sets are mutually exclusive and collectively exhaustive). Once the two sets of towns have been determined, the two facilities will operate as separate and independent entities. Each facility operates in the following way. Ambulances are stationed at each medical facility and travel to incidents
(and back) along shortest paths.
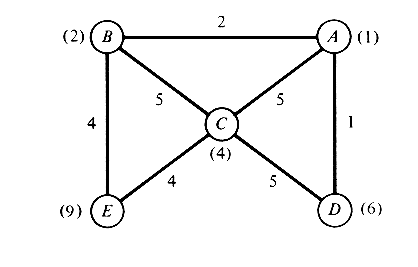
Once a call for service is received, and provided that an ambulance is available, an ambulance is immediately dispatched to the caller. The ambulance spends exactly 4 minutes at the scene of the call for all calls and then travels back to the medical facility (travel takes exactly the same time both ways). As soon as an ambulance returns to its origin, it immediately becomes available to respond to the next call. Calls for service that are received when no ambulances are available are placed in a first-come, first-served queue and eventually receive service. No calls for service are ever lost.
|