


7.2.3 Identifying the Zones Where Events OccurWe have just seen how to generate events that are geographically distributed among and within zones in a city in accordance with some prespecified probability law. The reverse question is the following: "Given a point (x, y), in which geographical zone is it contained?" Clearly, the point-polygon method is also helpful in answering this question: it can be applied to each zone in turn, until a positive result is obtained. If the polygons to be tested, however, are many and have a relatively large number of sides, the computer time for this search will be excessive. The search can be made more efficient by again embedding each reporting
zone in the smallest rectangle that contains it, just as before (Figure
7.16). For any particular zone, denote the respective vertices of this
rectangle as follows:(xmin, ymin), (xmax, ymin),
(xmax, ymax), (xmin, ymax)
For the point (x, y)
to be within the zone, the following inequalities must be satisfied:
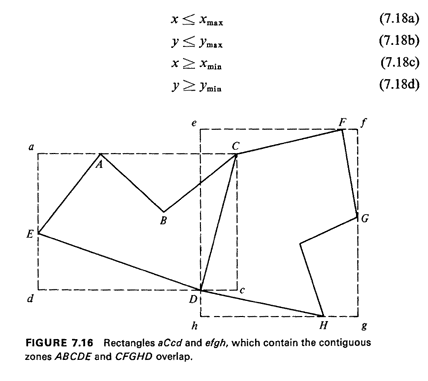
For large cities, the test indicated by inequality (7.18a) fails about 50 percent of the time, causing immediate rejection of the zone in question. If inequality (7.18a) is satisfied, inequality (7.18b) also has a conditional rejection rate of approximately 50 percent. The complete point-polygon procedure need be carried out only for those zones which satisfy inequalities (7.18), thus greatly decreasing the search time spent on obvious bad choices. It should be noted, in any event, that more than one candidate zone may satisfy inequalities (7.18), owing to the likely overlaps of the zone-containing rectangles as shown in Figure 7.16. Identifying the zone in which a point (x, y) is contained is likely to be a task that must be repeated a very large number of times in the course of a simulation. In that case, the procedure described above can be speeded up further by creating sorted lists, one each for the xmax, ymax, xmin, ymin coordinates of the vertices of the zone-containing rectangles. This can be done by using our efficient divide-and-conquer sorting algorithm. The identification of the rectangles (and zones) that satisfy inequalities (7.18) can then be accomplished quickly from the sorted lists, through use of our efficient searching algorithm. |