UOR_7.2.4

7.2.4 Do n Line Segments Intersect?

Suppose now that we are given n straight-line segments on a plane with each segment specified by its two end points. An interesting question then is: Do any of these line segments intersect? The straightforward approach requires 0(n₂) time: there are n(n - 1)/2 possible pairs of line segments which must be checked for intersections, and checking for the intersection of any given pair of line segments requires constant time. Once again, however, the most straightforward approach is not the most efficient one. We describe next an algorithm that requires 0(n log₂ n) time [SHAM 76] to answer the problem: "Is there at least one intersection? If so, identify one." In the x-y coordinate system we shall call the left (right) end point of a given line segment that end point of the segment with the smaller (larger) value of the x-coordinate.⁶ Suppose now that we begin "sweeping" a vertical line along the x-axis (Figure 7.17). Two line segments S and T are then said to be comparable at x = x₁ if they are both intersected by the vertical line at x = x1 The segments are consecutive if S is immediately above or immediately below T; in the former case we write S = above (T, x₁), in the latter S = below (T, x₁). Note that it is possible that no line segment will be above and/or below a line segment T for some or all values of x.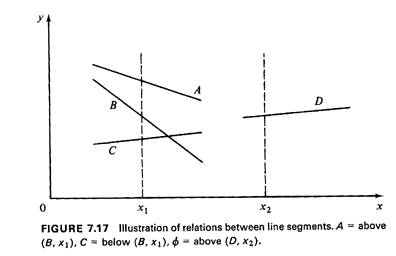

The key observation leading to the algorithm below is that if two line segments S and T intersect for some value of x = x₁, they must be consecutive⁷ for some range of x ‹ x₁. The algorithm thus concentrates on those line segments which become consecutive for some range of values of x.

The algorithm begins by sorting the 2n end points from left to right according to the values of their x-coordinates and then sweeps through the 2n end points from left to right. During the sweep, the algorithm maintains a list of current line segments which is sorted according to the order in which the line segments intersect the vertical sweep line. This sorted list is updated every time an end point is encountered: if the end point is a left end point, the corresponding line segment is added to the sorted list at the appropriate place; if it is a right end point, it is deleted from the list (see also Figure 7.18). The algorithm performs a check on whether two line segments intersect only when they become consecutive in the sorted list of line segments. It stops and returns the names of two intersecting line segments as soon as it finds an intersection.

We can now present the details of the algorithm:

Algorithm for the Intersection of Line Segments (Algorithm 7.1)

STEP 1: Sort the x-coordinates of the 2n end points of the line segments from left to right. Begin processing the 2n end points at the leftmost end point.
STEP 2: Let x_i denote the x-coordinate of the end point currently being processed and X the line segment corresponding to that end point.

1. If this is the left end point of X: a. Add X to the sorted list of current line segments, at its appropriate place according to the y-coordinate of the end point. b. If Y = above (X, x_i), check to determine if Y and X intersect. If they do, stop and return " Y and X." If they do not, continue. c. If Z = below (X, x_i), check to determine if Z and X intersect. If they do, stop and return "Z and X." If they do not, go to Step 3. 2. If this is the right end point of X: If Y = above (X, x_i) and Z = below (X, x_i), check whether Y and Z intersect. If they do, stop and return " Y and Z." If they do not, delete X from the list of current line segments.
STEP 3: If the last end point processed was the rightmost end point, stop and return "no intersection." If not, go to the next end point (to the right) and return to Step 2.

To prove that this algorithm works, (i.e., that it finds an intersection if there is at least one), it is sufficient to show (see Problem 7.5) that if the algorithm is not stopped when it finds its first intersection, it is guaranteed to find eventually the leftmost intersection of the line segments. This statement emphasizes the fact that the first intersection discovered by Algorithm 7.1 is not necessarily the leftmost intersection. 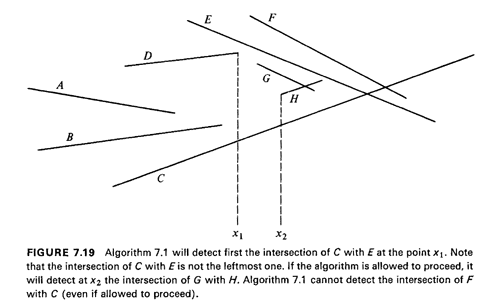This peculiarity is illustrated in Figure 7.19. Another peculiarity of Algorithm 7.1 is that, if allowed to process all end points, it may "miss" some intersections (see again Figure 7.19), although, as we just stated, it will never miss the leftmost one.

What is the computational complexity of Algorithm 7.1 ? Step 1 requires O(n log₂ n) time for sorting the 2n end points. [It actually requires 0(2n log 2n), but remember that in the theory of computational complexity 0(2n) is equivalent to O(n).] The addition (or deletion) of line segments to (or from) the sorted list of current line segments in Step 2 requires O(log₂ n) time, since the sorted list can contain at most n line segments at any time. Checking whether two line segments intersect requires constant time (i.e., is independent of n). Since in the worse case, when there is no intersection, Step 2 must be repeated 2n times, Step 2 also consumes a total time which is O(n log₂ n). Noting that Step 3 is trivial and will be repeated 2n times in the worst case, we thus conclude that Algorithm 7.1 is O(n log₂ n), as suggested initially.

⁶ If a line segment happens to be vertical, we can adopt any convenient convention for distinguishing between a left and a right end point.

⁷ With the exception of special cases in which 3 or more line segments intersect at the same point.