The Definition of Differentiation

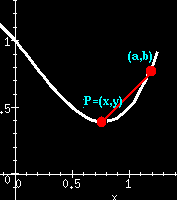
The essence of calculus is the derivative. The derivative is the instantaneous rate of change of a function with respect to one of its variables. This is equivalent to finding the slope of the tangent line to the function at a point. Let's use the view of derivatives as tangents to motivate a geometric definition of the derivative.

We want to find the slope of the tangent line to a graph at the point P. We can approximate the slope by drawing a line through the point P and another point nearby, and then finding the slope of that line, called a secant line. The slope of a line is determined using the following formula (m represents slope) :

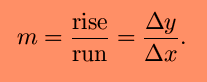
Let P = (x,y) and Q := (a,b). Let

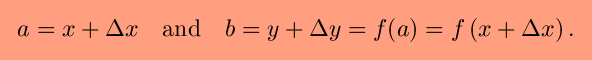
Then the slope of the line

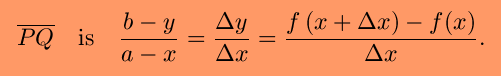
Now, we chose an arbitrary interval to be Delta-x. How does the size of Delta-x affect our estimate of the slope of the tangent line? The smaller Delta-x is, the more accurate this approximation is. There is a wonderful animation of this by Douglas Arnold. Look at it here. You can see on the left of the animation how Delta-x decreases, causing the secant line the approach the tangent, where it zooms in on the right. Another animation of this (also from Douglas Arnold) is here.

What we want to do is decrease the size of Delta-x as much as possible. We do this by taking the limit as Delta-x approaches zero. In the limit, assuming the limit exists, we will find the exact slope of the tangent line to the curve at the given point. This value is the derivative;

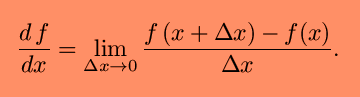
There are a few different, but equivalent, versions of this definition. In more general considerations, h is often used in place of Delta-x. Or Delta-y is used in place of

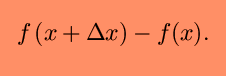
This leads to three commonly used ways of expressing the definition of the derivative:

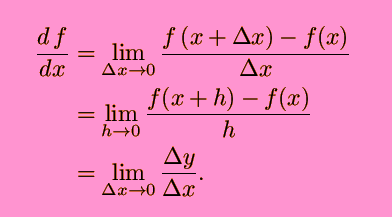
Notation relating to the derivative | When is a function differentiable?

Back to the Calculus page | Back to the World Web Math top page

watko@mit.edu

Last modified October 14, 1999.