The Squeeze Theorem Applied to Useful Trig Limits

Suggested Prerequesites: The Squeeze Theorem, An Introduction to Trig

There are several useful trigonometric limits that are necessary for eveluating the derivatives of trigonometric functions. Let's start by stating some (hopefully) obvious limits:

lim x
→ 0 sin &sp; x &sp;=&sp; 0

lim x
→ 0 cos &sp; x &sp;=&sp; 1

lim x
→ 0 tan &sp; x &sp;=&sp; 0

Since each of the above functions is continuous about x = 0, the value the limit at x = 0 is the value of the function at x= 0. This follows from the definition of limits.

In order to evaluate the derivatives of sin and cosine we need to evaluate

lim x → 0 sin &sp; x x &sp;

and

&sp; lim x → 0 1  - cos &sp;x x

In order to do this, need the following theorem of geometry:

If x is the measure of the central angle of a circle of radius r, then the area A of the sector determined by x is
A = r²x/2

Let's start by looking at $lim x → 0 sin &sp;
x x$ .

If $0 < t <
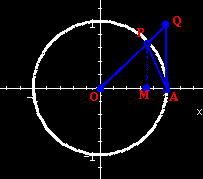π/2$ , then we have the situation in the figure to the left. Assume the circle is a unit circle, defined by x = cos t, y = sin t.

If A₁ is the area of the triangle AOP, A₂ is the area of the circular sector AOP, and A₃ is the area of the triangle AOQ,

A₁ < A₂ < A₃.

The area of a triangle equals one half the base times the height. Using this, and the above theorem for the area of a sector of a circle, we obtain:

	$A$ ₁ &sp;=&sp; 12 (OA) (MP) &sp;=&sp; 12 (1) (y) &sp;=&sp; 12&sp; sin &sp;t
	$A$ ₂ &sp;=&sp; 12 r^2^t &sp;=&sp; 12 (1)^2^t &sp;=&sp; 12 t
	$A_3_ &sp;=&sp; 12 (OA) (AQ) &sp;=&sp; 12 tan &sp; t$
Thus:	$12 sin &sp; t &sp;<&sp; 12 t &sp;<&sp; 12 tan &sp; t$

We divide by

12 sin&sp;t

and use the fact that tan x = sin x / cos x:

1 &sp;<&sp; t sin &sp;t &sp;<&sp; 1 cos &sp;t

which is equivalent to

1 &sp;>&sp; sin &sp;t t &sp;>&sp; cos &sp; t

Now, what about $- π 2 &sp;<&sp; t
&sp;<&sp; 0$ , which is the same as $0
&sp;<&sp; -t &sp;<&sp; π 2$ , then

1 &sp;>&sp; sin (-t) t &sp;>&sp; cos (-t)

which reduced to the previous inequality. Now, since

lim t →0 1 &sp;=&sp; 1 &sp;

and

lim t →0 cos &sp; t &sp;=&sp; 1

by the Squeeze Theorem is must be true that

lim t →0 sin &sp; t t &sp;=&sp; 1

What about

lim x →0 1  - cos &sp;t t

? Well, we do some algebraic manipulatons:

$1 - cos &sp;t t &sp;$	$=&sp; (1 - cos &sp;t t) (1 + cos &sp;t 1 + cos &sp;t)$
	$=&sp; 1 - cos^2^t t(1 + cos &sp;t)$
	$=&sp; sin^2^t t(1 + cos &sp;t)$
	$=&sp; (sin &sp;t t) (sin &sp;t 1 + cos &sp;t)$

Therefore:

$lim t→0 1 - cos &sp;t t &sp;$	$lim t→0 (sin &sp;t t &sp; sin &sp;t 1 + cos &sp;t)$
	$=&sp; (lim t→0 sin &sp;t t) (lim t→0 sin &sp;t 1 + cos &sp;t)$
	$=&sp; (1) (0 (1)(1)) &sp;=&sp; (1)(0) &sp;=&sp; 0$

To summarize the results of this page:

lim t→0 sin &sp;t t &sp;=&sp; 1

$lim t→0 1 - cos &sp;t t &sp;=&sp;
0$

Back to the Calculus page | Back to the World Web Math top page

jjnichol@mit.edu