 The Critical Point Test
The Critical Point Test
Prequisites: Partial Derivatives
So, Say a point P0=(a1,a,2,...an
,)
is a maximum point (or a minimum pont), of the equation
y= f(x1,x,2,...xn,)
. Then if we hold (x2,...xn)
fixed at (a2,...an) ,
f becomes a function of x1 only, with a maximum at
x1=a1.
Therefore at this point 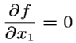 .
.
Likewise,
fx2=0,
fx3=0, ...
fxn=0 at point P.
A Critical Point is any point that satisfies these n
equations. Alternately, the critical point is any point on our
n-dimensional surface whose tangential n-1 surface is
parallel to the x1-axis, x2-axis,
... , and
xn-axis. We can determine critical points
(a1,a2,... an)
by solving these n equations for the n unknowns .
For example, say
f(x,y)=x5+y4-5x-32y. Then,
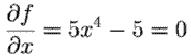 ,
,
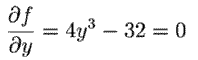 .
.
Solving for real critical points, we get (1,2) and (-1,2). But
are these points minimas or maxima, or neither? We notice
that the point x=1 is a minimum for the first equation and the
point y=2 is a minimum for the second equation. Therefore, the
point (1,2) is a minimum for
f(x,y)=x5+y4-5x-32y
. On the other hand, the point x=-1 is a maximum for the first
equation. Thus, this surface, viewed along the x-axis, comes to
a maximum, while viewed along the y-axis, comes to a minimum. The
critical point of (-1,2) is neither a minimum nor a maximum point for
the surface. It is a saddle point . Below are images of a
minimum, a maximum, and a saddle point critical point for a
two-variable function.


In
the next section
we will deal with one method
of figuring out whether a point is a minimum, maximum, or neither.
Vector Calculus Index |
World Web Math Main Page
watko@athena.mit.edu
Last modified November 5, 1998
 The Critical Point Test
The Critical Point Test The Critical Point Test
The Critical Point Test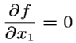 .
.
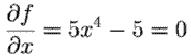 ,
,
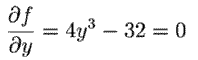 .
.

