Introduction to Minimization and Maximization

``Extremize f,'' said the text.
I at once partial f partial x'd.
I zeroed it, sighed,
partial f partial y'd,
But solving these two had me vexed.
-- Elizabeth Haley, haley@husc.harvard.edu

In Min/Max of basic calculus we covered how to find the minimums and maximums of single variable functions. Finding the minimum and maximums of two or more variable fuctions can be much more complicated. Say we have a function y=f(x1, x2, . . . , xn) and suppose it has a maximum at the point P0=(a1, a2, . . ., an) in the interior of its domain.

This means that for some neighborhood of P0,

is defined and

Of course, if P0 were a minimum, the last condition would be reversed.

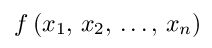
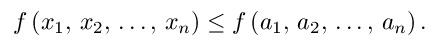
Note that he above definition of maximum allows a maximum point to not be isolated. That is, a maximum point could be part of a curve or plane of maximum points. Not all texts use this same definition; using

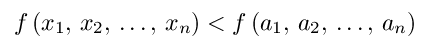
in the above would preclude non-isolated extremes.

Finding a function's critical points helps us to find its minimum and maximum points.

Vector Calculus Index | World Web Math Main Page

thing@athena.mit.edu
watko@athena.mit.edu
Last modified 8 August 1997