| Home | All Classes | Main Classes | Annotated | Grouped Classes | Functions |
The QWMatrix class specifies 2D transformations of a coordinate system. More...
#include <qwmatrix.h>
The standard coordinate system of a paint device has the origin located at the top-left position. X values increase to the right; Y values increase downward.
This coordinate system is the default for the QPainter, which renders graphics in a paint device. A user-defined coordinate system can be specified by setting a QWMatrix for the painter.
Example:
MyWidget::paintEvent( QPaintEvent * )
{
QPainter p; // our painter
QWMatrix m; // our transformation matrix
m.rotate( 22.5 ); // rotated coordinate system
p.begin( this ); // start painting
p.setWorldMatrix( m ); // use rotated coordinate system
p.drawText( 30,20, "detator" ); // draw rotated text at 30,20
p.end(); // painting done
}
A matrix specifies how to translate, scale, shear or rotate the graphics; the actual transformation is performed by the drawing routines in QPainter and by QPixmap::xForm().
The QWMatrix class contains a 3x3 matrix of the form:
| m11 | m12 | 0 |
| m21 | m22 | 0 |
| dx | dy | 1 |
A matrix transforms a point in the plane to another point:
x' = m11*x + m21*y + dx
y' = m22*y + m12*x + dy
The point (x, y) is the original point, and (x', y') is the transformed point. (x', y') can be transformed back to (x, y) by performing the same operation on the inverted matrix.
The elements dx and dy specify horizontal and vertical translation. The elements m11 and m22 specify horizontal and vertical scaling. The elements m12 and m21 specify horizontal and vertical shearing.
The identity matrix has m11 and m22 set to 1; all others are set to 0. This matrix maps a point to itself.
Translation is the simplest transformation. Setting dx and dy will move the coordinate system dx units along the X axis and dy units along the Y axis.
Scaling can be done by setting m11 and m22. For example, setting m11 to 2 and m22 to 1.5 will double the height and increase the width by 50%.
Shearing is controlled by m12 and m21. Setting these elements to values different from zero will twist the coordinate system.
Rotation is achieved by carefully setting both the shearing factors and the scaling factors. The QWMatrix also has a function that sets rotation directly.
QWMatrix lets you combine transformations like this:
QWMatrix m; // identity matrix
m.translate(10, -20); // first translate (10,-20)
m.rotate(25); // then rotate 25 degrees
m.scale(1.2, 0.7); // finally scale it
Here's the same example using basic matrix operations:
double a = pi/180 * 25; // convert 25 to radians
double sina = sin(a);
double cosa = cos(a);
QWMatrix m1(0, 0, 0, 0, 10, -20); // translation matrix
QWMatrix m2( cosa, sina, // rotation matrix
-sina, cosa, 0, 0 );
QWMatrix m3(1.2, 0, 0, 0.7, 0, 0); // scaling matrix
QWMatrix m;
m = m3 * m2 * m1; // combine all transformations
QPainter has functions to translate, scale, shear and rotate the coordinate system without using a QWMatrix. Although these functions are very convenient, it can be more efficient to build a QWMatrix and call QPainter::setWorldMatrix() if you want to perform more than a single transform operation.
See also QPainter::setWorldMatrix(), QPixmap::xForm(), Graphics Classes, and Image Processing Classes.
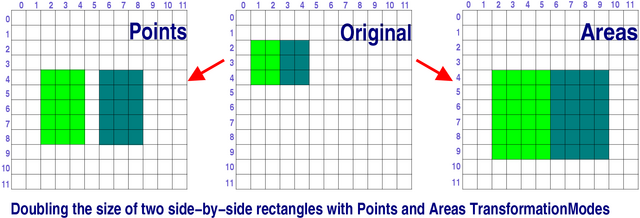
QWMatrix offers two transformation modes. Calculations can either be done in terms of points (Points mode, the default), or in terms of area (Area mode).
In Points mode the transformation is applied to the points that mark out the shape's bounding line. In Areas mode the transformation is applied in such a way that the area of the contained region is correctly transformed under the matrix.
Example:
Suppose we have a rectangle, QRect( 10, 20, 30, 40 ) and a transformation matrix QWMatrix( 2, 0, 0, 2, 0, 0 ) to double the rectangle's size.
In Points mode, the matrix will transform the top-left (10,20) and the bottom-right (39,59) points producing a rectangle with its top-left point at (20,40) and its bottom-right point at (78,118), i.e. with a width of 59 and a height of 79.
In Areas mode, the matrix will transform the top-left point in the same way as in Points mode to (20/40), and double the width and height, so the bottom-right will become (69,99), i.e. a width of 60 and a height of 80.
Because integer arithmetic is used (for speed), rounding differences mean that the modes will produce slightly different results given the same shape and the same transformation, especially when scaling up. This also means that some operations are not commutative.
Under Points mode, matrix * ( region1 | region2 ) is not equal to matrix * region1 | matrix * region2. Under Area mode, matrix * (pointarray[i]) is not neccesarily equal to (matrix * pointarry)[i].
Returns the matrix's determinant.
Returns the horizontal translation.
Returns the vertical translation.
If the matrix is singular (not invertible), the identity matrix is returned.
If invertible is not 0: the value of *invertible is set to TRUE if the matrix is invertible; otherwise *invertible is set to FALSE.
See also isInvertible().
Example: t14/cannon.cpp.
See also reset().
Returns TRUE if the matrix is invertible; otherwise returns FALSE.
See also invert().
Returns the X scaling factor.
Returns the vertical shearing factor.
Returns the horizontal shearing factor.
Returns the Y scaling factor.
*tx = m11*x + m21*y + dx (rounded to the nearest integer)
*ty = m22*y + m12*x + dy (rounded to the nearest integer)
Examples: t14/cannon.cpp and xform/xform.cpp.
Transforms ( x, y ) to ( *tx, *ty ) using the following formulae:
*tx = m11*x + m21*y + dx
*ty = m22*y + m12*x + dy
This is an overloaded member function, provided for convenience. It behaves essentially like the above function.
Transforms p to using the formulae:
retx = m11*px + m21*py + dx (rounded to the nearest integer)
rety = m22*py + m12*px + dy (rounded to the nearest integer)
This function is obsolete. It is provided to keep old source working. We strongly advise against using it in new code.
Please use QWMatrix::mapRect() instead.
Note that this method does return the bounding rectangle of the r, when shearing or rotations are used.
This is an overloaded member function, provided for convenience. It behaves essentially like the above function.
Returns the point array a transformed by calling map for each point.
This is an overloaded member function, provided for convenience. It behaves essentially like the above function.
Transforms the region r.
Calling this method can be rather expensive, if rotations or shearing are used.
The bounding rectangle is returned if rotation or shearing has been specified.
If you need to know the exact region rect maps to use operator*().
See also operator*().
Polygons and rectangles behave slightly differently when transformed (due to integer rounding), so matrix.map( QPointArray( rect ) ) is not always the same as matrix.mapToPolygon( rect ).
Returns the transformed rectangle rect.
A rectangle which has been rotated or sheared may result in a non-rectangular region being returned.
Calling this method can be expensive, if rotations or shearing are used. If you just need to know the bounding rectangle of the returned region, use mapRect() which is a lot faster than this function.
See also QWMatrix::mapRect().
All elements are set to zero, except m11 and m22 (scaling) which are set to 1.
See also isIdentity().
Returns a reference to the matrix.
See also translate(), scale(), and shear().
Examples: canvas/canvas.cpp, desktop/desktop.cpp, drawdemo/drawdemo.cpp, t14/cannon.cpp, and xform/xform.cpp.
Returns a reference to the matrix.
See also translate(), shear(), and rotate().
Examples: canvas/canvas.cpp, fileiconview/qfileiconview.cpp, movies/main.cpp, qmag/qmag.cpp, showimg/showimg.cpp, and xform/xform.cpp.
See also QWMatrix::TransformationMode.
Returns a reference to the matrix.
See also translate(), scale(), and rotate().
Examples: drawdemo/drawdemo.cpp and xform/xform.cpp.
See also QWMatrix::TransformationMode.
Returns a reference to the matrix.
See also scale(), shear(), and rotate().
Examples: canvas/canvas.cpp, drawdemo/drawdemo.cpp, t14/cannon.cpp, and xform/xform.cpp.
Writes the matrix m to the stream s and returns a reference to the stream.
See also Format of the QDataStream operators.
Reads the matrix m from the stream s and returns a reference to the stream.
See also Format of the QDataStream operators.
This file is part of the Qt toolkit. Copyright © 1995-2003 Trolltech. All Rights Reserved.
| Copyright © 2003 Trolltech | Trademarks | Qt version 3.1.2
|