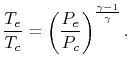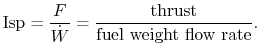14.1 Thrust and Specific Impulse for Rockets
Previously we used the steady flow energy equation to relate the
exhaust velocity of a rocket motor,
Figure 14.1, to the conditions in the
combustion chamber and the exit pressure.
Figure 14.1:
Schematic of rocket nozzle and combustion chamber
|
|
The steady flow energy equation
then with no heat transfer or shaft work,
which can be written as
and manipulated to obtain
using
Then considering the relationship we derived for thrust,
and assuming
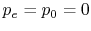 , then
, then
and
Rearranging,
Thus the specific impulse can be directly related to the exhaust
velocity leaving the rocket,
UnifiedTP
|


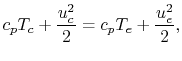
![$\displaystyle u_e = \sqrt{2c_p T_c\left[1-\left(\frac{p_e}{p_c}\right)^{\frac{\gamma-1}{\gamma}}\right]},$](img1660.png)