16.4 Thermal Resistance Circuits
There is an electrical analogy
with conduction heat transfer that can be exploited in problem
solving. The analog of 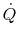 is current, and the analog of the
temperature difference,
is current, and the analog of the
temperature difference, 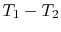 , is voltage difference. From
this perspective the slab is a pure resistance to heat transfer and
we can define
, is voltage difference. From
this perspective the slab is a pure resistance to heat transfer and
we can define
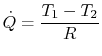 |
(16..21) |
where 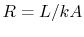 , the thermal resistance. The thermal resistance
, the thermal resistance. The thermal resistance 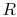 increases as
increases as 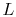 increases, as
increases, as 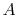 decreases, and as
decreases, and as 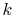 decreases.
decreases.
Figure 16.6:
Heat transfer across a
composite slab (series thermal resistance)
|
|
The concept of a thermal resistance circuit allows ready analysis of
problems such as a composite slab (composite planar heat transfer
surface). In the composite slab shown in
Figure 16.6, the heat flux is
constant with 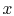 . The resistances are in series and sum to
. The resistances are in series and sum to
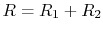 . If
. If 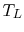 is the temperature at the left, and
is the temperature at the left, and 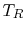 is the
temperature at the right, the heat transfer rate is given by
is the
temperature at the right, the heat transfer rate is given by
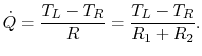 |
(16..22) |
Figure 16.7:
Heat transfer for a wall with
dissimilar materials (parallel thermal resistance)
|
|
Another example is a wall with a dissimilar material such as a bolt
in an insulating layer. In this case, the heat transfer resistances
are in parallel. Figure 16.7
shows the physical configuration, the heat transfer paths and the
thermal resistance circuit.
For this situation, the total heat flow 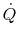 is made up of the
heat flow in the two parallel paths,
is made up of the
heat flow in the two parallel paths,
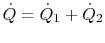 , with the total resistance given by
, with the total resistance given by
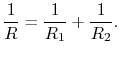 |
(16..23) |
More complex configurations can also be examined; for example, a
brick wall with insulation on both sides
(Figure 16.8).
Figure 16.8:
Heat transfer
through an insulated wall
|
|
The overall thermal resistance is given by
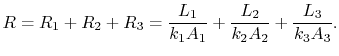 |
(16..24) |
Some representative values for the brick and insulation thermal
conductivity are:
Using these values, and noting that
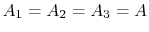 , we obtain
, we obtain
This is a series circuit
so
Figure 16.9:
Temperature
distribution through an insulated wall
|
|
The temperature is continuous in the wall and the intermediate
temperatures can be found from applying the resistance equation
across each slab, since 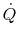 is constant across the slab. For
example, to find
is constant across the slab. For
example, to find 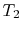 :
:
This yields
 or
or
 .
.
The same procedure gives
 . As sketched in
Figure 16.9, the larger drop
is across the insulating layer even though the brick layer is much
thicker.
. As sketched in
Figure 16.9, the larger drop
is across the insulating layer even though the brick layer is much
thicker.
Muddy Points
What do you mean by continuous?
(MP 16.4)
Why is temperature continuous in the composite wall problem? Why is
it continuous at the interface between two materials?
(MP 16.5)
Why is the temperature gradient  not continuous?
(MP 16.6)
not continuous?
(MP 16.6)
Why is 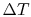 the same for the two elements in a parallel
thermal circuit? Doesn't the relative area of the bolt to the wood
matter? (MP 16.7)
the same for the two elements in a parallel
thermal circuit? Doesn't the relative area of the bolt to the wood
matter? (MP 16.7)
UnifiedTP
| 

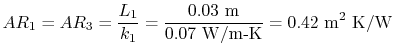
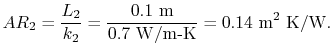
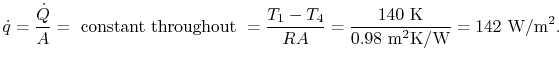
![]() is constant across the slab. For
example, to find
is constant across the slab. For
example, to find ![]() :
:
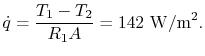
![]() . As sketched in
Figure 16.9, the larger drop
is across the insulating layer even though the brick layer is much
thicker.
. As sketched in
Figure 16.9, the larger drop
is across the insulating layer even though the brick layer is much
thicker.
![]() not continuous?
(MP 16.6)
not continuous?
(MP 16.6)
![]() the same for the two elements in a parallel
thermal circuit? Doesn't the relative area of the bolt to the wood
matter? (MP 16.7)
the same for the two elements in a parallel
thermal circuit? Doesn't the relative area of the bolt to the wood
matter? (MP 16.7)