18.1 Temperature Distributions in the Presence of Heat Sources
There are a number of situations in which there are sources of heat in the domain of interest.
Examples are:
- Electrical heaters where electrical energy is converted
resistively into heat.
- Nuclear power supplies.
- Propellants where
chemical energy is the source.
These situations can be analyzed by looking at a model problem of a
slab with heat sources 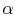 (W/m3) distributed
throughout. We take the outside walls to be at temperature
(W/m3) distributed
throughout. We take the outside walls to be at temperature 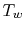 and
we will determine the maximum internal temperature.
and
we will determine the maximum internal temperature.
Figure 18.1:
Slab with heat sources
[Overall configuration]
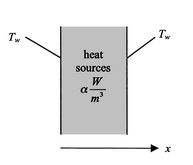
[Infinitesimal slice]
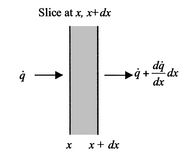
|
With reference to Figure 18.1(b), a
steady-state energy balance yields an equation for the heat flux,
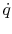 :
:
or
There is a change in heat flux with 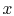 due to the presence of the
heat sources. The equation for the temperature is
due to the presence of the
heat sources. The equation for the temperature is
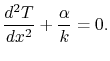 |
(18..1) |
Equation (18.1) can be integrated
once,
and again to give
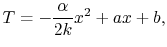 |
(18..2) |
where 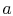 and
and 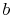 are constants of integration. The boundary
conditions imposed are
are constants of integration. The boundary
conditions imposed are
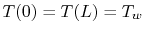 . Substituting these into
Equation (18.2) gives
. Substituting these into
Equation (18.2) gives 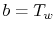 and
and
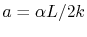 . The temperature distribution is thus
. The temperature distribution is thus
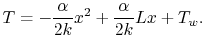 |
(18..3) |
Writing (18.3) in a normalized,
non-dimensional fashion gives a form that exhibits in a more useful
manner the way in which the different parameters enter the problem:
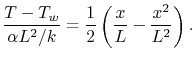 |
(18..4) |
Figure 18.2:
Temperature distribution for
slab with distributed heat sources
|
|
This distribution is sketched in
Figure 18.2. It is symmetric about the
mid-plane at 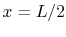 , with half the energy due to the sources
exiting the slab on each side.
, with half the energy due to the sources
exiting the slab on each side.
The heat flux at the side of the slab, 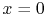 , can be found by
differentiating the temperature distribution and evaluating at
, can be found by
differentiating the temperature distribution and evaluating at 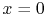 :
:
This is half of the total heat generated within the slab. The
magnitude of the heat flux is the same at 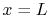 , although the
direction is opposite.
, although the
direction is opposite.
A related problem would be one in which there were heat flux
(rather than temperature) boundary conditions at 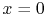 and
and 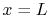 , so that
, so that 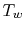 is not known. We again determine the maximum
temperature. At
is not known. We again determine the maximum
temperature. At 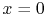 and
and 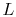 , the heat flux and temperature are
continuous so
, the heat flux and temperature are
continuous so
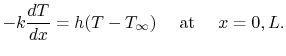 |
(18..5) |
Referring to the temperature distribution of
Equation (18.2) gives for the two
terms in Equation (18.5),
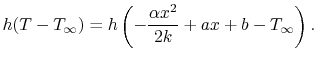 |
(18..6) |
Evaluating (18.6) at 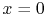 and
and 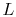 allows determination of the two constants
allows determination of the two constants 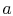 and
and 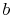 . This
is left as an exercise for the reader.
. This
is left as an exercise for the reader.
Muddy Points
For an electric heated strip embedded between two layers, what would
the temperature distribution be if the two side temperatures were
not equal? (MP 18.1)
UnifiedTP
|

